题目内容
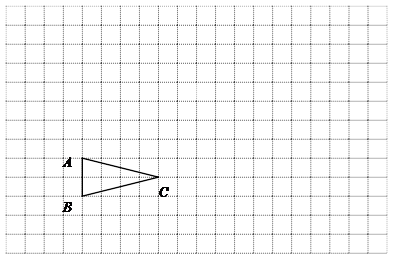
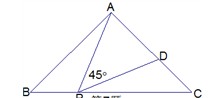
已知：如图，△ABC中，∠ABC＝2∠C，BD平分∠ABC．求证：AB·BC＝AC·CD
∵∠ABC=2∠C，BD平分∠ABC，
∴∠ABD=∠DBC=∠C，
∴BD=CD，
在△ABD和△ACB中，
，
∴△ABD∽△ACB（AA），
∴
=
，
即AB•BC=AC•BD，
∴AB•BC=AC•CD．
∴∠ABD=∠DBC=∠C，
∴BD=CD，
在△ABD和△ACB中，
，∴△ABD∽△ACB（AA），
∴
=，即AB•BC=AC•BD，
∴AB•BC=AC•CD．
根据∠ABC=2∠C，BD平分∠ABC可以求出∠ABD=∠DBC=∠C，然后证明出BD=CD与△ABD与△ACB相似，在根据相似三角形的对应边成比例列式整理即可得证．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
轴上的一个动点，M是线段AC的中点.把线段AM进行以A为旋转中心、向顺时针方向旋转90°的旋转变换得到AB.过B作
轴的垂线，两直线交于点D，直线DB交
，
，则
？
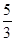
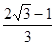
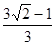
的照射下在墙上形成影子，.现测得
则这个三角尺的面积与它在墙上所形成影子图形的面积之比是 ．
；（4分）