题目内容
9.解方程组$\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{2}=8}\\{3x-2y=7}\end{array}\right.$.分析 首先利用①×6去分母,然后再利用③×2+②×3可得y的值,进而可得x的值.
解答 解:$\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{2}=8①}\\{3x-2y=7②}\end{array}\right.$,
①×6得:2x+3y=48③,
③×2得:4x+6y=96④,
②×3得:9x-6y=21⑤,
④+⑤得:13x=117,
x=9,
把x=9代入②得:27-2y=7,
y=10,
∴方程组的解为$\left\{\begin{array}{l}{x=9}\\{y=10}\end{array}\right.$.
点评 此题主要考查了二元一次方程组的解法,关键是掌握用加减法解二元一次方程组的一般步骤:①方程组的两个方程中,如果同一个未知数的系数既不相等又不互为相反数,就用适当的数去乘方程的两边,使某一个未知数的系数相等或互为相反数.②把两个方程的两边分别相减或相加,消去一个未知数,得到一个一元一次方程.③解这个一元一次方程,求得未知数的值.④将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数的值.⑤把所求得的两个未知数的值写在一起,就得到原方程组的解.

练习册系列答案
相关题目
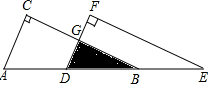 如图将Rt△ABC沿斜边AB向右平移5cm,得到Rt△DEF.已知AB=10cm,BC=8cm.求图中阴影部分三角形的周长.
如图将Rt△ABC沿斜边AB向右平移5cm,得到Rt△DEF.已知AB=10cm,BC=8cm.求图中阴影部分三角形的周长.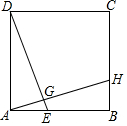 如图,正方形ABCD中,H在BC上,DE⊥AH交AB于点E,交AH于点G,若AB=3,BH=1.
如图,正方形ABCD中,H在BC上,DE⊥AH交AB于点E,交AH于点G,若AB=3,BH=1.