题目内容
7.△ABC中,∠C是最小内角.若过顶点B的一条直线把这个三角形分成两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为△ABC的关于点B的伴侣分割线.例如:如图1,△ABC中,∠A=90°,∠C=20°,若过顶点B的一条直线BD交AC于点D,且∠DBC=20°,则直线BD是△ABC的关于点B的伴侣分割线.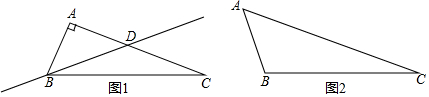
(1)如图2,△ABC中,∠C=20°,∠ABC=110°.请在图中画出△ABC关于点B的伴侣分割线,并注明角度;(画图工具不限)
(2)△ABC中,设∠B的度数为y,最小内角∠C的度数为x.试探索y与x应满足什么要求时,△ABC存在关于点B的伴侣分割线.
分析 (1)根据伴侣分割线的定义,把∠ABC分成90°角和20°角即可;
(2)设BD为△ABC的伴侣分割线,分以下两种情况:△BDC是等腰三角形,△ABD是直角三角形;△BDC是直角三角形,△ABD是等腰三角形,分别进行计算即可.
解答 解:(1)如图所示,BD即为△ABC关于点B的伴侣分割线;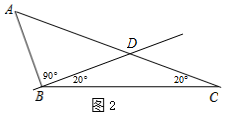
(2)设BD为△ABC的伴侣分割线,分两种情况:
①△BDC是等腰三角形,△ABD是直角三角形,
易知∠C和∠DBC必为底角,
∴∠DBC=∠C=x.
当∠A=90°时,△ABC存在伴侣分割线,
此时y=90°-x,
当∠ABD=90°时,△ABC存在伴侣分割线,
此时y=90°+x,
当∠ADB=90°时,△ABC存在伴侣分割线,
此时x=45°且90°≥y>45°;
②△BDC是直角三角形,△ABD是等腰三角形,
当∠DBC=90°时,若BD=AD,则△ABC存在伴侣分割线,
此时180°-x-y=y-90°,
∴y=135°-$\frac{1}{2}$x,
当∠BDC=90°时,若BD=AD,则△ABC存在伴侣分割线,
此时∠A=45°,
∴y=135°-x.
综上所述,当y=90°-x,或y=90°+x,或x=45°且y>x且90°≥y>45°,或y=135°-$\frac{1}{2}$x,或y=135°-x时,△ABC存在伴侣分割线.
点评 此题主要考查了复杂作图,解决此类题目需要熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.解题的关键是正确理解题意,了解伴侣分割线的意义.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
 已知实数a,b,c在数轴上的对应点如图所示,化简:$\root{3}{(a-b)^{3}}$-|b+c|-$\sqrt{(a-c)^{2}}$.
已知实数a,b,c在数轴上的对应点如图所示,化简:$\root{3}{(a-b)^{3}}$-|b+c|-$\sqrt{(a-c)^{2}}$. 如图,AB是⊙O的直径,∠CAB=60°,则∠D=30度.
如图,AB是⊙O的直径,∠CAB=60°,则∠D=30度.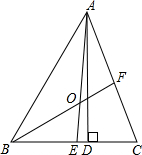 如图,在△ABC中,AD是高,AE,BF是角平分线,AE和BF交于点O,∠BAC=58°,∠BOA=125°,求∠C和∠DAE的度数.
如图,在△ABC中,AD是高,AE,BF是角平分线,AE和BF交于点O,∠BAC=58°,∠BOA=125°,求∠C和∠DAE的度数.