题目内容
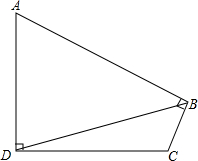 在四边形ABCD中,∠ABC=∠CDA=90°,AD=DC=5,AB=7,BC=1,求BD的值.
在四边形ABCD中,∠ABC=∠CDA=90°,AD=DC=5,AB=7,BC=1,求BD的值.考点:勾股定理
专题:
分析:根据四边形的内角和等于360°求出∠BAD+∠C=180°,把△BCD绕点D逆时针旋转90°可得等腰直角△BDE,求出BE,然后根据等腰直角三角形的性质求解即可.
解答: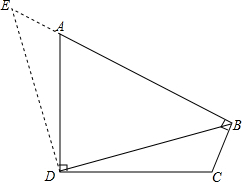 解:∵∠ABC=∠CDA=90°,
解:∵∠ABC=∠CDA=90°,
∴∠BAD+∠C=180°,
把△BCD绕点D逆时针旋转90°得等腰直角△BDE,
由旋转的性质,BD=BE,∠BDE=90°,
∴△BDE是等腰直角三角形,
∵AB=7,BC=1,
∴BE=1+7=8,
∴BD=
BE=
×8=4
.
 解:∵∠ABC=∠CDA=90°,
解:∵∠ABC=∠CDA=90°,∴∠BAD+∠C=180°,
把△BCD绕点D逆时针旋转90°得等腰直角△BDE,
由旋转的性质,BD=BE,∠BDE=90°,
∴△BDE是等腰直角三角形,
∵AB=7,BC=1,
∴BE=1+7=8,
∴BD=
| ||
| 2 |
| ||
| 2 |
| 2 |
点评:本题考查了勾股定理,等腰直角三角形的判定与性质,利用旋转作辅助线构造出以BD为直角边的等腰直角三角形是解题的关键.

练习册系列答案
相关题目