题目内容
△ABC中,a=15,b=17,∠A为定值,若满足上述条件的△ABC的∠C唯一存在,则tan∠C的值是________.

分析:根据∠A为定值,又a<b,那么∠A必为锐角,要使∠C有唯一值,则以点C为圆心,15为半径的圆与AB相切.得到直角△ABC,然后求出∠C的正切.
解答:
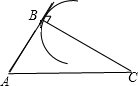 解:∵a<b,∠A为定值,
解:∵a<b,∠A为定值,∴∠A为锐角.
要使∠C有唯一的值,则以点C为圆心,15为半径画的弧与AB相切.如图所示:
得到直角△ABC,AC=17,BC=15,
则:AB=
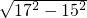 =8,
=8,∴tanC=
 =
= .
.故答案是:
 .
.点评:本题考查的是锐角三角函数的定义,根据题目的条件确定∠A为锐角,又因为∠C唯一确定,所以以点C为圆心,15为半径的圆与AB相切,得到直角△ABC,然后根据正切的定义求出∠C的正切值.

练习册系列答案
相关题目
 如图,在△ABC中,BC=15,B1、B2、…B9、C1、C2、…C9分别是AB、AC的10等分点,则B1C1+B2C2+…+B9C9的值是( )
如图,在△ABC中,BC=15,B1、B2、…B9、C1、C2、…C9分别是AB、AC的10等分点,则B1C1+B2C2+…+B9C9的值是( )| A、45 | B、55 | C、67.5 | D、135 |
 △ABC中,AB=15,BC=12,AC=9,圆O是△ABC的内切圆,则图中阴影部分的面积为
△ABC中,AB=15,BC=12,AC=9,圆O是△ABC的内切圆,则图中阴影部分的面积为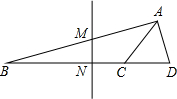 D,MN垂直平分BD,垂足为N,交AB于点M.
D,MN垂直平分BD,垂足为N,交AB于点M.