题目内容
如图,长为4、宽为1的矩形OABC在直角坐标系中,其一个顶点B恰在函数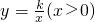 的图象上.
的图象上.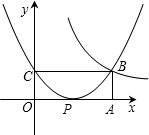
(1)k的值为______;
(2)试确定A,B,C三点的坐标;
(3)若抛物线y=ax2+bx+c经过B,C两点,且顶点P在x轴上,试确定其解析式.
解:(1)由反比例函数解析式,可知k=xy=OA×AB=4×1=4,
故答案为:4;
(2)∵四边形OABC为矩形,且OA=4,AB=1,
∴A(4,0),B(4,1),C(0,1);
(3)由抛物线的对称性可知,抛物线顶点P为线段OA的中点,
∴P(2,0),
设抛物线为y=a(x-2)2,将C(0,1)代入,得
4a=1,
解得a= ,
,
∴y= (x-2)2,
(x-2)2,
即y= x2-x+1.
x2-x+1.
分析:(1)根据k=xy=OA×AB,求k的值;
(2)根据矩形的长、宽,可求A,B,C三点的坐标;
(2)由抛物线的对称性可知,抛物线顶点坐标为P(2,0),设抛物线的顶点式,将C(0,1)代入即可.
点评:本题考查了二次函数的综合运用.关键是根据矩形,抛物线的轴对称性求点的坐标.
故答案为:4;
(2)∵四边形OABC为矩形,且OA=4,AB=1,
∴A(4,0),B(4,1),C(0,1);
(3)由抛物线的对称性可知,抛物线顶点P为线段OA的中点,
∴P(2,0),
设抛物线为y=a(x-2)2,将C(0,1)代入,得
4a=1,
解得a=
 ,
,∴y=
 (x-2)2,
(x-2)2,即y=
 x2-x+1.
x2-x+1.分析:(1)根据k=xy=OA×AB,求k的值;
(2)根据矩形的长、宽,可求A,B,C三点的坐标;
(2)由抛物线的对称性可知,抛物线顶点坐标为P(2,0),设抛物线的顶点式,将C(0,1)代入即可.
点评:本题考查了二次函数的综合运用.关键是根据矩形,抛物线的轴对称性求点的坐标.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
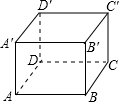 如图,地面上有一个长方体,一只蜘蛛在这个长方体的顶点A处,一滴水珠在这个长方形的顶点C′处,已知长方体的长为6m,宽为5m,高为3m,蜘蛛要沿着长方体的表面从A处爬到C′处,则蜘蛛爬行的最短距离为( )
如图,地面上有一个长方体,一只蜘蛛在这个长方体的顶点A处,一滴水珠在这个长方形的顶点C′处,已知长方体的长为6m,宽为5m,高为3m,蜘蛛要沿着长方体的表面从A处爬到C′处,则蜘蛛爬行的最短距离为( ) 25、如图,长为10cm,宽为6cm的长方形,在4个角剪去4个边长为x的小正方形,按折痕做一个有底无盖的长方形盒子,试求盒子的体积.
25、如图,长为10cm,宽为6cm的长方形,在4个角剪去4个边长为x的小正方形,按折痕做一个有底无盖的长方形盒子,试求盒子的体积.

 如图是长为5,宽为4,高为3的长方体,一只蚂蚁从顶点A沿长方体的表面爬行到顶点B的最短距离是( )
如图是长为5,宽为4,高为3的长方体,一只蚂蚁从顶点A沿长方体的表面爬行到顶点B的最短距离是( )