题目内容
5．一个平行四边形的周长是50，面积是50$\sqrt{3}$，且一个内角为60°，求这个平行四边形一组邻边的长．分析 过A作AE⊥BC于E，求得AE，然后根据题意列方程组即可解出结果．
解答 
解：如图：过A作AE⊥BC于E，
设AB=x，BC=y，
∵∠B=60°，
∴AE=AB•sin60°=$\frac{\sqrt{3}x}{2}$，
∵平行四边形的周长是50，面积是50$\sqrt{3}$，
∴$\left\{\begin{array}{l}{2x+2y=50}\\{\frac{\sqrt{3}}{2}xy=50\sqrt{3}}\end{array}\right.$，
∴$\left\{\begin{array}{l}{x=20}\\{y=5}\end{array}\right.$或$\left\{\begin{array}{l}{x=5}\\{y=20}\end{array}\right.$，
∴平行四边形一组邻边的长为5和20．
点评 本题考查了平行四边形的性质，三角函数，掌握平行四边形的性质是解题的关键．
练习册系列答案
习题精选系列答案
相关题目
13．
如图，在平面直角坐标系中，四边形ABCD的顶点均在网格点上，将四边形ABCD先向左平移3个单位，再向上平移2个单位，那么点A的对应点A′的坐标是（ ）
如图，在平面直角坐标系中，四边形ABCD的顶点均在网格点上，将四边形ABCD先向左平移3个单位，再向上平移2个单位，那么点A的对应点A′的坐标是（ ）| A． | （6，1） | B． | （0，1） | C． | （0，-3） | D． | （6，-3） |
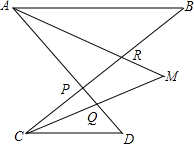如图，∠B=36°，∠D=50°，AM，CM分别平分∠BAD和∠BCD，AM交BC于点R，CM交AD于点Q，BC与AD交于点P，求∠M的度数．
