题目内容
如图，四边形ABCD的对角线AC与BD相交于点O，∠1＝∠2,∠3＝∠4．
求证：(1)△ABC≌△ADC ； (2)BO=DO．
证明：在△ABC和△ADC中，
∵∠1＝∠2, AC=AC，∠3＝∠4．
∴△ABDC≌△BAD． ∴AB=AD ．
∴△ABD为等腰三角形
在等腰△ADB中 ∵∠1＝∠2,
∴BO=DO．(三线合一)
练习册系列答案
相关题目
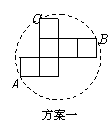
操作：小明准备制作棱长为1cm的正方体纸盒，现选用一些废弃的纸片进行如下设计：
 | |||
 | |||
纸片利用率=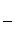
×100%
发现：（1）方案一中的点A.B恰好为该圆一直径的两个端点．你认为小明的这个发现是否正确，请说明理由．
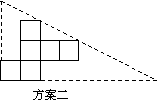
（2）小明通过计算，发现方案一中纸片的利用率仅约为38.2%．请帮忙计算方案二的利用率，并写出求解过程．
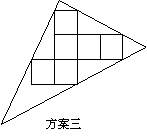
探究：（3）小明感觉上面两个方案的利用率均偏低，又进行了新的设计（方案三），请直接写出方案三的利用率．
|
 |
轴对称的点的坐标是 ． 
②试求甲车在离B地多远处与返程中的乙车相遇?
的度数为（ ）
恰逢阴天，于是两人商定改用下面方法：如图，亮亮蹲在地上，颖颖站在亮亮和楼之间，两人适当调整自己的位置，当楼的顶部
，颖颖的头顶
及亮亮的眼睛
恰在一条直线上时，两人分别标定自己的位置
，
．然后测出两人之间的距离
，颖颖与楼之间的距离
（
在一条直线上），颖颖的身高
，亮亮蹲地观测时眼睛到地面的距离
．
．