题目内容
19. 如图,⊙O是△ABC的外接圆,圆心O在AB上,M是OA上一点,过M作AB的垂线交BC的延长线于点E,过点C作⊙O的切线,交ME于点F.
如图,⊙O是△ABC的外接圆,圆心O在AB上,M是OA上一点,过M作AB的垂线交BC的延长线于点E,过点C作⊙O的切线,交ME于点F.(1)求证:EF=CF;
(2)若∠B=2∠A,AB=4,且AC=CE,求BM的长.
分析 (1)延长FC至H,由AB是⊙O的直径,得出∠ACB=90°,由EM⊥AB,得出∠EMB=∠ACB=90°,证得△ABC∽△EMB,得出∠CEF=∠CAB,由弦切角定理得出∠CAB=∠BCH,由对顶角相等得出∠BCH=∠ECF,推出∠CEF=∠ECF,即可得出结论;
(2)利用含30度的直角三角形三边的性质得出BC=$\frac{1}{2}$AB=2,AC=$\sqrt{3}$BC=2$\sqrt{3}$,则CE=2$\sqrt{3}$,所以BE=BC+CE=2+2$\sqrt{3}$,然后在Rt△BEM中计算出BM=$\frac{1}{2}$BE即可.
解答 (1)证明:延长FC至H,如图所示:
∵⊙O是△ABC的外接圆,圆心O在AB上,
∴AB是⊙O的直径,
∴∠ACB=90°,
∵EM⊥AB,
∴∠EMB=∠ACB=90°,
∵∠ABC=∠EBM,
∴△ABC∽△EMB,
∴∠CEF=∠CAB,
∵FC是⊙O的切线,
∴∠CAB=∠BCH,
∵∠BCH=∠ECF
∴∠CAB=∠ECF,
∴∠CEF=∠ECF,
∴EF=CF;
(2)解:∵∠ACB=90°,∠B=2∠A,
∴∠B=60°,∠A=30°,
在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,
∴BC=$\frac{1}{2}$AB=2,AC=$\sqrt{3}$BC=2$\sqrt{3}$,
∵AC=CE,
∴CE=2$\sqrt{3}$,
∴BE=BC+CE=2+2$\sqrt{3}$,
在Rt△BEM中,∠BME=90°,∠BEM=∠A=30°
∴BM=$\frac{1}{2}$BE=1+$\sqrt{3}$.
点评 本题考查了切线的性质、含30度的角直角三角形的性质、相似三角形的判定与性质、弦切角定理等知识;熟练掌握弦切角定理与含30度的角直角三角形的性质是解决问题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 9件 | B. | 10件 | C. | 11件 | D. | 12件 |
 如图,过边长为3的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,且CQ=PA,连接PQ交AC于点D,则DE的长为( )
如图,过边长为3的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,且CQ=PA,连接PQ交AC于点D,则DE的长为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
| A. | y2>y1>y3 | B. | y3>y2>y1 | C. | y1>y2>y3 | D. | y3>y1>y2 |
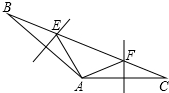 如图,在△ABC中,AB和AC的垂直平分线分别交BC于E、F,若∠BAC=130°,则∠EAF=80°.
如图,在△ABC中,AB和AC的垂直平分线分别交BC于E、F,若∠BAC=130°,则∠EAF=80°.
 如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )
如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )