题目内容
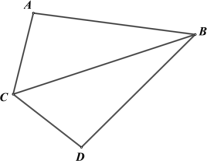
【题目】如图,二次函数y=ax2+bx+c(a≠0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为﹣1,3,与y轴负半轴交于点C.以下五个结论:①2a+b=0;②a+b+c>0;③4a+b+c>0;④只有当a=![]() 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值可以有两个.那么,其中正确的结论是_____.
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值可以有两个.那么,其中正确的结论是_____.

【答案】①④⑤
【解析】
先根据图象与x轴的交点A,B的横坐标分别为-1,3确定出AB的长及对称轴,再由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:①∵图象与x轴的交点A,B的横坐标分别为﹣1,3,
∴AB=4,
∴对称轴x=![]() =
=![]() =1,
=1,
即2a+b=0;
故①正确;
②由抛物线的开口方向向上可推出a>0,而![]() >0
>0
∴b<0,
∵对称轴x=1,
∴当x=1时,y<0,
∴a+b+c<0;
故②错误;
③∵图象与x轴的交点A,B的横坐标分别为﹣1,3,
∴a﹣b+c=0,9a+3b+c=0,
∴10a+2b+2c=0,
∴5a+b+c=0,
∴a+4a+b+c=0,
∵a>0,
∴4a+b+c<0,
故③错误;
④要使△ABD为等腰直角三角形,必须保证D到x轴的距离等于AB长的一半;
D到x轴的距离就是当x=1时y的值的绝对值.
当x=1时,y=a+b+c,
即|a+b+c|=2,
∵当x=1时y<0,
∴a+b+c=﹣2,
又∵图象与x轴的交点A,B的横坐标分别为﹣1,3,
∴当x=﹣1时y=0即a﹣b+c=0;
x=3时y=0.
∴9a+3b+c=0,
解这三个方程可得:b=﹣1,a=![]() ,c=﹣
,c=﹣![]() ;
;
⑤要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,
当AB=BC=4时,
∵AO=1,△BOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16﹣9=7,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=﹣![]() ,
,
与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=![]() ;
;
同理当AB=AC=4时,
∵AO=1,△AOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16﹣1=15,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=﹣![]()
与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=![]() ;
;
同理当AC=BC时
在△AOC中,AC2=1+c2,
在△BOC中BC2=c2+9,
∵AC=BC,
∴1+c2=c2+9,此方程无解.
经解方程组可知只有两个a值满足条件.
故⑤正确.
故答案为:①④⑤.

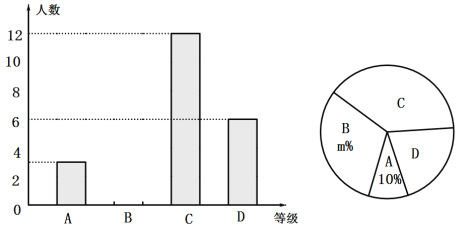
【题目】为进一步提升学生的法律素质,中学组织学生开展《宪法》知识竞赛,该学校随机抽取部分学生的成绩并进行统计分析,以了解学生的法律知识水平.根据这些学生的竞赛成绩分布情况,将竞赛成绩分为甲、乙、丙、丁、戊五个等级.图表如下:
等级 | 分数/分 | 频数 | 各组总分/分 |
甲 |
| 39 | 2184 |
乙 |
| 75 | 5175 |
丙 |
| 120 | 9720 |
丁 |
|
| 4050 |
戊 |
| 21 | 2037 |

(1)求![]() 的值;
的值;
(2)竞赛成绩的中位数落在哪个等级?
(3)求这组竞赛成绩的平均值.