题目内容
已知AD是△ABC的高(点D不与B,C重合),E是线段AD上一点,且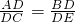 ,给出下列结论:①∠BED=∠ACB;②BE⊥AC;③CE⊥AB;④△ADC∽△BDE;⑤△DEC∽△DBA.其中正确的是
,给出下列结论:①∠BED=∠ACB;②BE⊥AC;③CE⊥AB;④△ADC∽△BDE;⑤△DEC∽△DBA.其中正确的是
- A.①②④
- B.①③⑤
- C.①②③
- D.④⑤
A
分析:先画出图形,利用两边及其夹角法可判断△ADC∽△BDE,结合相似三角形的对应角相等的性质可判断①②④正确;
解答: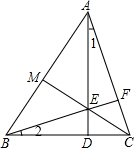 解:如图所示:
解:如图所示:
∵∠BDE=∠ADC=90°,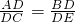 ,
,
∴△ADC∽△BDE,故④正确;
∴∠BED=∠ACB,故①正确;
∴∠1=∠2,
∵∠1+∠ACD=90°,
∴∠2+∠ACD=90°,
∴BE⊥AC,故②正确;
综上可得①②④正确.
故选A.
点评:本题考查了相似三角形的判定与性质,解答本题的关键是利用两边及其夹角的办法判定△ADC∽△BDE,要求同学们熟练相似三角形的性质,对应边成比例,对应角相等.
分析:先画出图形,利用两边及其夹角法可判断△ADC∽△BDE,结合相似三角形的对应角相等的性质可判断①②④正确;
解答:
 解:如图所示:
解:如图所示:∵∠BDE=∠ADC=90°,
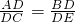 ,
,∴△ADC∽△BDE,故④正确;
∴∠BED=∠ACB,故①正确;
∴∠1=∠2,
∵∠1+∠ACD=90°,
∴∠2+∠ACD=90°,
∴BE⊥AC,故②正确;
综上可得①②④正确.
故选A.
点评:本题考查了相似三角形的判定与性质,解答本题的关键是利用两边及其夹角的办法判定△ADC∽△BDE,要求同学们熟练相似三角形的性质,对应边成比例,对应角相等.

练习册系列答案
相关题目
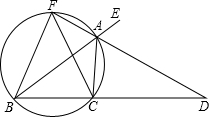 于点F,连接FB、FC.
于点F,连接FB、FC. 3、如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:①AG:AD=1:2;②GE:BE=1:4;③GE:BE=3:4,其中正确的为( )
3、如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:①AG:AD=1:2;②GE:BE=1:4;③GE:BE=3:4,其中正确的为( )
