题目内容
10. 如图,六边形ABCDEF的内角都相等,CF∥AB.
如图,六边形ABCDEF的内角都相等,CF∥AB.(1)求∠FCD的度数;
(2)求证:AF∥CD.
分析 (1)先求六边形ABCDEF的每个内角的度数,根据平行线的性质可求∠B+∠BCF=180°,再根据四边形的内角和是360°,求∠FCD的度数,从而求解.
(2)先根据四边形内角和求出∠AFC=60°,再根据平行线的判定即可求解.
解答 解:(1)∵六边形ABCDEF的内角相等,
∴∠B=∠A=∠BCD=120°,
∵CF∥AB,
∴∠B+∠BCF=180°,
∴∠BCF=60°,
∴∠FCD=60°;
(2)∵∠AFC=360°-120°-120°-60°=60°,
∴∠AFC=∠FCD,
∴AF∥CD.
点评 考查了多边形内角与外角和平行线的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
20.用代数式表示a与5的差的2倍,正确的是( )
| A. | a-5×2 | B. | a+5×2 | C. | 2(a-5) | D. | 2(a+5) |
18.点A(-3,-4)关于y轴对称点是( )
| A. | (3,-4) | B. | (-3,4) | C. | (3,4) | D. | (-4,3) |
5.对于有理数a,b,定义一种新运算,规定a※b=-a2-b,则(-2)※(-3)=( )
| A. | 7 | B. | 1 | C. | -7 | D. | -1 |
15.在-2017、0、-3、2017这四个数中,最小的数是( )
| A. | -2017 | B. | 0 | C. | -3 | D. | 2017 |
2.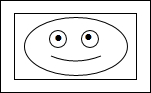 某校团委准备举办学生绘画展览,为美化画面,在长8dm、宽为5dm的矩形内画面四周镶上宽度相等的彩纸,并使彩纸的面积等于22dm2(如图),若设彩纸的宽度为x分米,则可得方程为( )
某校团委准备举办学生绘画展览,为美化画面,在长8dm、宽为5dm的矩形内画面四周镶上宽度相等的彩纸,并使彩纸的面积等于22dm2(如图),若设彩纸的宽度为x分米,则可得方程为( )
 某校团委准备举办学生绘画展览,为美化画面,在长8dm、宽为5dm的矩形内画面四周镶上宽度相等的彩纸,并使彩纸的面积等于22dm2(如图),若设彩纸的宽度为x分米,则可得方程为( )
某校团委准备举办学生绘画展览,为美化画面,在长8dm、宽为5dm的矩形内画面四周镶上宽度相等的彩纸,并使彩纸的面积等于22dm2(如图),若设彩纸的宽度为x分米,则可得方程为( )| A. | 40-10x-16x=18 | B. | (8-x)(5-x)=18 | C. | (8-2x)(5-2x)=18 | D. | 40-5x-8x+4x2=22 |
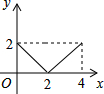
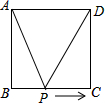 如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )


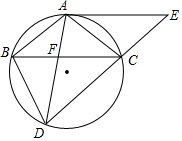 如图,四边形ABDC内接于⊙O,AB=AC,且AB∥CD、过点A作⊙O的切线AE与DC的延长线交于点E,AD与BC交于点F.
如图,四边形ABDC内接于⊙O,AB=AC,且AB∥CD、过点A作⊙O的切线AE与DC的延长线交于点E,AD与BC交于点F. 已知:如图,AB∥CD,OA=OC.求证:OB=OD.
已知:如图,AB∥CD,OA=OC.求证:OB=OD.