题目内容
如图，在一次函数y=﹣x+6的图象上取一点P，作PA⊥x轴于点A，PB⊥y轴于点B，且矩形PBOA的面积为5，则在x轴的上方满足上述条件的点P的个数共有（ ）
A．1个 B． 2个 C． 3个 D． 4个
C 解：①当0＜x＜6时，设点P（x，﹣x+6），
∴矩形PBOA的面积为5，
∴x（﹣x+6）=5，化简x2﹣6x+5=0，解得x1=1，x2=5，
∴P1（1，5），P2（5，1），
②当x＜0时，设
点P（x，﹣x+6），
∴矩形PBOA的面积为5，
∴﹣x（﹣x+6）=5，化简x2﹣6x﹣5=0，解得x3=3﹣
，x4=3+（舍去），
∴P3（3﹣，3+），
∴在x轴的上方满足上述条件的点P的个数共有3个．
练习册系列答案
相关题目
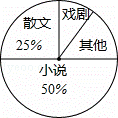
八年级一班开展了“读一本好书”的活动，班委会对学生阅读书籍的情况进行了问卷调查，问卷设置了“小说”、“戏剧”、“散文”、“其他”
四个类别，每位同学仅选一项，根
据调查结果绘制了不完整的频数分布表和扇形统计图．根据图表提供的信息，回答下列问题：
| 类别 | 频数（人数） | 频率 |
| 小说 | 0.5 | |
| 戏剧 | 4 | |
| 散文 | 10 | 0.25 |
| 其他 | 6 | |
| 合计 | m | 1 |
（1）计算m= 40 ；
（2）在扇形统计图中，“其他”类所占的百分比为 15% ；
（3）在调查问卷中，甲、乙、丙、丁四位同学选择了“戏剧”类，现从中任意选出2名同学参加学校的戏剧社团，请用画树状图或列表的方法，求选取的2人恰好是乙和丙的概率．
款外套9月份投放市场的批发价为150元/件，出现购销两旺态势，10月份进入批发淡季，厂方决定采取打折促销．已知生产一件外套需人工等固定费用14元，为确保每件外套的利润不低于30元．
+3
=5
D． 
÷
；