Question

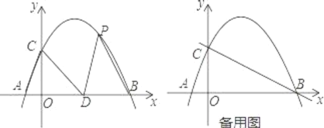
【题目】如图，在平面直角坐标系中，点A的坐标为轴于点，反比例函数的图像的一支分别交于点，延长交反比例函数的图像的另一支于点E，已知D的纵坐标为．

（1）求反比例函数的解析式及直线OA的解析式；

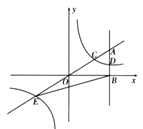
（2）连接BC，已知，求

（3）若在轴上有两点，将直线绕点旋转，仍与交于，能否构成以为顶点的四边形为菱形，如果能请求出的值，如果不能说明理由．

Answer 1

【答案】（1），；（2）24；（3）不能，理由见解析

【解析】

（1）根据已知条件可求A、D的坐标，用待定系数法即求出反比例函数解析式；由点A坐标求直线OA的解析式．

（2）把直线OA与反比例函数解析式联立方程组，即求出交点C,E的坐标，再把△CEB分成△COB与△EOB，以OB为公共底，点C和点E纵坐标的绝对值为高即求出三角形面积．

（3）若为菱形，则对角线互相垂直，但CE不与x轴垂直，矛盾，故不能成为菱形．

解：（1）因为点A的坐标为轴于B，所以

，B（8,0）

点D在反比例函数的图象上

所以反比例函数的解析式为

设直线OA的解析式

解得

所以直线OA的解析式为；

（2）联立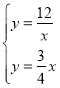，解得或

∴又

；

（3）因为所在直线不可能与轴垂直，即不能与垂直

所以为顶点的四边形不能是菱形．