ƒøƒĞ»ı
°æƒø°ø–¬∂®“£∫∂‘”Ğπÿ”Ğ![]() µƒ∫Ø ˝
µƒ∫Ø ˝![]() £¨Œ“√«≥∆∫Ø ˝
£¨Œ“√«≥∆∫Ø ˝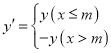 Œ™∫Ø ˝yµƒm∑÷∫Ø ˝£®∆‰÷–mŒ™≥£ ˝£©.
Œ™∫Ø ˝yµƒm∑÷∫Ø ˝£®∆‰÷–mŒ™≥£ ˝£©.
¿˝»Á£∫∂‘”Ğπÿ”Ğx“ª¥Œ∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝Œ™
∑÷∫Ø ˝Œ™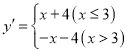
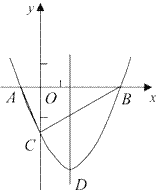
£®1£©»Ùµ„![]() ‘Ğπÿ”Ğxµƒ“ª¥Œ∫Ø ˝
‘Ğπÿ”Ğxµƒ“ª¥Œ∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝…œ£¨«Û
∑÷∫Ø ˝…œ£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©–¥≥ˆ∑¥±»¿˝∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝µƒÕºœÛ…œyÀÊxµƒ‘ˆ¥Û∂¯º–°µƒxµƒ»°÷µ∑∂Œß£∫ £ª
∑÷∫Ø ˝µƒÕºœÛ…œyÀÊxµƒ‘ˆ¥Û∂¯º–°µƒxµƒ»°÷µ∑∂Œß£∫ £ª
£®3£©»Ù![]() «∂˛¥Œ∫Ø ˝
«∂˛¥Œ∫Ø ˝![]() πÿ”Ğxµƒ
πÿ”Ğxµƒ![]() ∑÷∫Ø ˝£¨
∑÷∫Ø ˝£¨
¢Ÿµ±![]() ±£¨«Ûyµƒ»°÷µ∑∂Œß£ª
±£¨«Ûyµƒ»°÷µ∑∂Œß£ª
¢Ğµ±![]() ±£¨
±£¨![]() £¨‘Ú
£¨‘Ú![]() µƒ»°÷µ∑∂ŒßŒ™ £ª
µƒ»°÷µ∑∂ŒßŒ™ £ª
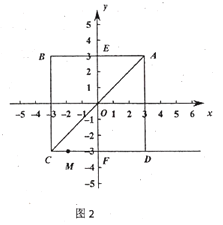
¢ğ»Ùµ„![]() £¨¡¨Ω·
£¨¡¨Ω·![]() £¨µ±πÿ”Ğ
£¨µ±πÿ”Ğ![]() µƒ∂˛¥Œ∫Ø ˝
µƒ∂˛¥Œ∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝£¨”Îœş∂ŒMN”–¡Ω∏ˆΩªµ„£¨÷±Ω”–¥≥ˆmµƒ»°÷µ∑∂Œß.
∑÷∫Ø ˝£¨”Îœş∂ŒMN”–¡Ω∏ˆΩªµ„£¨÷±Ω”–¥≥ˆmµƒ»°÷µ∑∂Œß.
°æ¥∞∏°ø£®1£©n=3£ª£®2£©![]() ªÚ
ªÚ![]() £ª£®3£©¢Ÿ
£ª£®3£©¢Ÿ![]() ªÚ
ªÚ![]() £ª¢Ğ
£ª¢Ğ![]() £ª¢ğm£º
£ª¢ğm£º![]() ªÚ
ªÚ![]() °İm£º
°İm£º![]() ªÚ
ªÚ![]() °İm.
°İm.
°æΩ‚Œˆ°ø
£®1£© ◊œ»–¥≥ˆ“ª¥Œ∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝£¨»ª∫ÛΩ´µ„P¥˙»Îº¥ø…«Û≥ˆn£ª
∑÷∫Ø ˝£¨»ª∫ÛΩ´µ„P¥˙»Îº¥ø…«Û≥ˆn£ª
£®2£© ◊œ»–¥≥ˆ∑¥±»¿˝∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝£¨»ª∫Û∏˘æı∑¥±»¿˝∫Ø ˝µƒ‘ˆº–‘Ω¯––≈–∂®£ª
∑÷∫Ø ˝£¨»ª∫Û∏˘æı∑¥±»¿˝∫Ø ˝µƒ‘ˆº–‘Ω¯––≈–∂®£ª
£®3£©¢Ÿ ◊œ»–¥≥ˆ∂˛¥Œ∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝£¨»ª∫Û∏˘æıxµƒ»°÷µ∑∂ŒßΩ·∫œ∂˛¥Œ∫Ø ˝µƒ–‘÷ ∑÷±«Û≥ˆ∂‘”¶µƒyµƒ»°÷µ∑∂Œßº¥ø…£ª
∑÷∫Ø ˝£¨»ª∫Û∏˘æıxµƒ»°÷µ∑∂ŒßΩ·∫œ∂˛¥Œ∫Ø ˝µƒ–‘÷ ∑÷±«Û≥ˆ∂‘”¶µƒyµƒ»°÷µ∑∂Œßº¥ø…£ª
¢Ğ ◊œ»«Û≥ˆµ±![]() ±£¨
±£¨![]() µƒ»°÷µ∑∂ŒßŒ™
µƒ»°÷µ∑∂ŒßŒ™![]() £¨µ±
£¨µ±![]() ±£¨
±£¨![]() £¨»ª∫Û∏˘æı
£¨»ª∫Û∏˘æı![]() ø…÷™£¨«Û≥ˆ
ø…÷™£¨«Û≥ˆ![]() ±
±![]() µƒ÷µ‘Ğ-3∫Õ-4÷ƺ‰£®∞¸∫¨-3∫Õ-4£©∂‘”¶µƒxµƒ»°÷µ∑∂Œßº¥ø…£ª
µƒ÷µ‘Ğ-3∫Õ-4÷ƺ‰£®∞¸∫¨-3∫Õ-4£©∂‘”¶µƒxµƒ»°÷µ∑∂Œßº¥ø…£ª
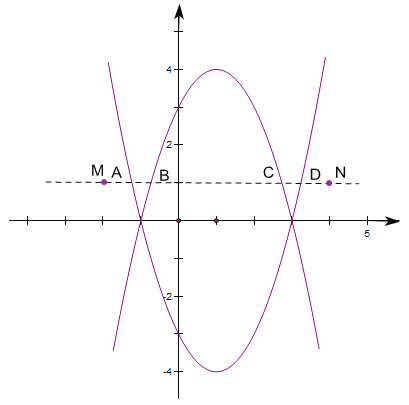
¢ğª≠≥ˆ![]() ∫Õ
∫Õ![]() µƒ∫Ø ˝ÕºœÒ£¨«Û≥ˆ¡Ω∫Ø ˝ÕºœÛ”Îy=1µƒΩªµ„µƒ∫·◊¯±Í£¨»ª∫ÛΩ·∫œ∫Ø ˝ÕºœÛ∑÷¿‡Ã÷¬ğ£¨∑÷±«Û≥ˆ‘Ğ≤ªÕ¨µƒ∑∂ŒßƒĞ”Îœş∂ŒMNµƒΩªµ„∏ˆ ˝£¨º¥ø…µ√µΩ∑˚∫œÃ‚“‚µƒmµƒ»°÷µ∑∂Œß.
µƒ∫Ø ˝ÕºœÒ£¨«Û≥ˆ¡Ω∫Ø ˝ÕºœÛ”Îy=1µƒΩªµ„µƒ∫·◊¯±Í£¨»ª∫ÛΩ·∫œ∫Ø ˝ÕºœÛ∑÷¿‡Ã÷¬ğ£¨∑÷±«Û≥ˆ‘Ğ≤ªÕ¨µƒ∑∂ŒßƒĞ”Îœş∂ŒMNµƒΩªµ„∏ˆ ˝£¨º¥ø…µ√µΩ∑˚∫œÃ‚“‚µƒmµƒ»°÷µ∑∂Œß.
Ω‚£∫£®1£©”…“‚µ√£∫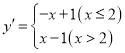 £¨
£¨
°ş![]() £¨
£¨
°‡∞—![]() ¥˙»Î
¥˙»Î![]() µ√
µ√![]() £¨
£¨
°‡![]() £ª
£ª
£®2£©”…“‚µ√£∫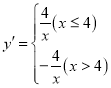 £¨
£¨
∏˘æı∫Ø ˝Ω‚Œˆ Ωø…÷™£¨µ±![]() ªÚ
ªÚ![]() ±£¨yÀÊxµƒ‘ˆ¥Û∂¯º–°£ª
±£¨yÀÊxµƒ‘ˆ¥Û∂¯º–°£ª
£®3£©¢Ÿ”…“‚µ√£∫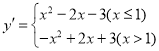 £¨
£¨
µ±![]() ±£¨
±£¨![]() µƒÕºœÛyÀÊxµƒ‘ˆ¥Û∂¯º–°£¨
µƒÕºœÛyÀÊxµƒ‘ˆ¥Û∂¯º–°£¨
∞—![]() ¥˙»Î
¥˙»Î![]() £¨ø…µ√
£¨ø…µ√![]() £¨
£¨
∞—![]() ¥˙»Î
¥˙»Î![]() £¨ø…µ√
£¨ø…µ√![]() £ª
£ª
µ±![]() ±£¨
±£¨![]() µƒÕºœÛyÀÊxµƒ‘ˆ¥Û∂¯º–°£¨
µƒÕºœÛyÀÊxµƒ‘ˆ¥Û∂¯º–°£¨
∞—![]() ¥˙»Î
¥˙»Î![]() £¨ø…µ√
£¨ø…µ√![]() £¨
£¨
∞—![]() ¥˙»Î
¥˙»Î![]() £¨ø…µ√
£¨ø…µ√![]() £¨
£¨
◊ğ…œ£¨![]() µƒ»°÷µ∑∂ŒßŒ™
µƒ»°÷µ∑∂ŒßŒ™![]() ªÚ
ªÚ![]() £ª
£ª
¢Ğ°ş∞—![]() ¥˙»Î
¥˙»Î![]() £¨ø…µ√
£¨ø…µ√![]() £¨
£¨
∞—![]() ¥˙»Î
¥˙»Î![]() £¨ø…µ√
£¨ø…µ√![]() £ª
£ª
°‡µ±![]() ±£¨
±£¨![]() µƒ»°÷µ∑∂ŒßŒ™
µƒ»°÷µ∑∂ŒßŒ™![]() £¨
£¨
”…¢Ÿ÷™£¨µ±![]() ±£¨
±£¨![]() £¨
£¨
∞—y£Ω£≠3¥˙»Î![]() £¨Ω‚µ√£∫
£¨Ω‚µ√£∫![]() £®∏∫÷µ“—…·»•£©£¨
£®∏∫÷µ“—…·»•£©£¨
∞—y£Ω£≠4¥˙»Î![]() £¨Ω‚µ√£∫
£¨Ω‚µ√£∫![]() £®∏∫÷µ“—…·»•£©£¨
£®∏∫÷µ“—…·»•£©£¨
°‡![]() µƒ»°÷µ∑∂ŒßŒ™
µƒ»°÷µ∑∂ŒßŒ™![]() £ª
£ª
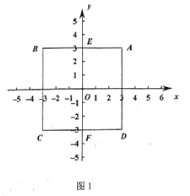
¢ğ»ÁÕºŒ™![]() ∫Õ
∫Õ![]() µƒ∫Ø ˝ÕºœÒ£¨A°¢B°¢C°¢D∑÷± «¡Ω∫Ø ˝ÕºœÛ”Îy=1µƒΩªµ„£¨
µƒ∫Ø ˝ÕºœÒ£¨A°¢B°¢C°¢D∑÷± «¡Ω∫Ø ˝ÕºœÛ”Îy=1µƒΩªµ„£¨
¡™¡¢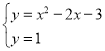 £¨Ω‚µ√£∫
£¨Ω‚µ√£∫![]() £¨
£¨
°‡Aµ„∫·◊¯±ÍŒ™![]() £¨Dµ„∫·◊¯±ÍŒ™
£¨Dµ„∫·◊¯±ÍŒ™![]() £¨
£¨
¡™¡¢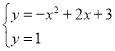 £¨Ω‚µ√£∫
£¨Ω‚µ√£∫![]() £¨
£¨
°‡Bµ„∫·◊¯±ÍŒ™![]() £¨Cµ„∫·◊¯±ÍŒ™
£¨Cµ„∫·◊¯±ÍŒ™![]() £¨
£¨
Ω·∫œ∫Ø ˝ÕºœÛ£¨∑÷¿‡Ã÷¬ğ£∫
¢Ÿµ±m£º![]() ±£¨πÿ”Ğ
±£¨πÿ”Ğ![]() µƒ∂˛¥Œ∫Ø ˝
µƒ∂˛¥Œ∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝£¨”Îœş∂ŒMN”–¡Ω∏ˆΩªµ„£ª
∑÷∫Ø ˝£¨”Îœş∂ŒMN”–¡Ω∏ˆΩªµ„£ª
¢Ğµ±![]() °İm£º
°İm£º![]() ±£¨πÿ”Ğ
±£¨πÿ”Ğ![]() µƒ∂˛¥Œ∫Ø ˝
µƒ∂˛¥Œ∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝£¨”Îœş∂ŒMN”–»˝∏ˆΩªµ„£ª
∑÷∫Ø ˝£¨”Îœş∂ŒMN”–»˝∏ˆΩªµ„£ª
¢ğµ±![]() °İm£º
°İm£º![]() ±£¨πÿ”Ğ
±£¨πÿ”Ğ![]() µƒ∂˛¥Œ∫Ø ˝
µƒ∂˛¥Œ∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝£¨”Îœş∂ŒMN”–¡Ω∏ˆΩªµ„£ª
∑÷∫Ø ˝£¨”Îœş∂ŒMN”–¡Ω∏ˆΩªµ„£ª
¢İ![]() °İm£º
°İm£º![]() ±£¨πÿ”Ğ
±£¨πÿ”Ğ![]() µƒ∂˛¥Œ∫Ø ˝
µƒ∂˛¥Œ∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝£¨”Îœş∂ŒMN”–“ª∏ˆΩªµ„£ª
∑÷∫Ø ˝£¨”Îœş∂ŒMN”–“ª∏ˆΩªµ„£ª
¢ıµ±![]() °İm ±£¨πÿ”Ğ
°İm ±£¨πÿ”Ğ![]() µƒ∂˛¥Œ∫Ø ˝
µƒ∂˛¥Œ∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝£¨”Îœş∂ŒMN”–¡Ω∏ˆΩªµ„£ª
∑÷∫Ø ˝£¨”Îœş∂ŒMN”–¡Ω∏ˆΩªµ„£ª
◊ğ…œÀ˘ ˆ£∫mµƒ»°÷µ∑∂Œß «m£º![]() ªÚ
ªÚ![]() °İm£º
°İm£º![]() ªÚ
ªÚ![]() °İm.
°İm.