题目内容
11.如图所示,用火柴棍拼成一排由三角形组成的图形,如果图形中含有2,3或4个三角形,分别需要多少根火柴棍?如果图形中含有n个三角形,需要多少根火柴棍?
分析 一个三角形时,将左边一根固定,后面每增加一个三角形就加2根火柴棍,据此可分别计算出有2,3或4个及n个三角形时,火柴棍数量.
解答 解:有1个三角形时,需要1+2=3根火柴棍,
有2个三角形时,需要1+2×2=5根火柴棍,
有3个三角形时,需要1+3×2=7根火柴棍,
有4个三角形时,需要1+4×2=9根火柴棍,
…
有n个三角形,需要1+n×2=2n+1根火柴棍.
答:如果图形中含有2,3或4个三角形,分别需要5、7、9根火柴棍,
如果图形中含有n个三角形,需要(2n+1)根火柴棍.
点评 本题考查了图形的变化规律,找出图形之间的联系是关键,并将得出的运算规律解决问题,属中档题.

练习册系列答案
相关题目
2. 如图,∠1=∠2,PC⊥OA,PD⊥OB,垂足分别为点C、D,则下列结论中错误的是( )
如图,∠1=∠2,PC⊥OA,PD⊥OB,垂足分别为点C、D,则下列结论中错误的是( )
 如图,∠1=∠2,PC⊥OA,PD⊥OB,垂足分别为点C、D,则下列结论中错误的是( )
如图,∠1=∠2,PC⊥OA,PD⊥OB,垂足分别为点C、D,则下列结论中错误的是( )| A. | PD=OD | B. | PC=PD | C. | ∠DPO=∠CPO | D. | OD=OC |
3.-$\frac{1}{2}$的倒数的相反数是( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
20. 如图,已知AB∥CD,DE⊥AC,垂足为E,∠A=130°,则∠D的度数是( )
如图,已知AB∥CD,DE⊥AC,垂足为E,∠A=130°,则∠D的度数是( )
 如图,已知AB∥CD,DE⊥AC,垂足为E,∠A=130°,则∠D的度数是( )
如图,已知AB∥CD,DE⊥AC,垂足为E,∠A=130°,则∠D的度数是( )| A. | 20° | B. | 40° | C. | 50° | D. | 70° |
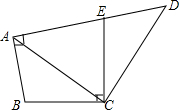 如图,四边形ABCD中,E点在AD上,∠BAE=∠BCE=90°,且BC=CE,AB=DE.
如图,四边形ABCD中,E点在AD上,∠BAE=∠BCE=90°,且BC=CE,AB=DE.