Question

4．在菱形ABCD中，对角线AC，BD的长分别是6和8，则菱形的周长是20．

Answer 1

分析 AC与BD相交于点O，如图，根据菱形的性质得AC⊥BD，OD=OB=$\frac{1}{2}$BD=4，OA=OC=$\frac{1}{2}$AC=3，AB=BC=CD=AD，则可在Rt△AOD中，根据勾股定理计算出AD=5，于是可得菱形ABCD的周长为20．

解答 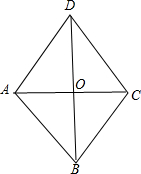解：AC与BD相交于点O，如图，
∵四边形ABCD为菱形，
∴AC⊥BD，OD=OB=$\frac{1}{2}$BD=4，OA=OC=$\frac{1}{2}$AC=3，AB=BC=CD=AD，
在Rt△AOD中，∵OA=3，OB=4，
∴AD=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∴菱形ABCD的周长=4×5=20．
故答案为20．

点评 本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．