题目内容
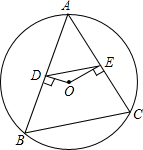 如图,△ABC为⊙O的内接三角形,O为圆心.OD⊥AB,垂足为D,OE⊥AC,垂足为E,若DE=3,则BC长为( )
如图,△ABC为⊙O的内接三角形,O为圆心.OD⊥AB,垂足为D,OE⊥AC,垂足为E,若DE=3,则BC长为( )| A、6 | B、3 | C、8 | D、10 |
考点:垂径定理,三角形中位线定理
专题:计算题
分析:由OD⊥AB,OE⊥AC,根据垂径定理得到AD=DB,AE=CE,则根据三角形中位线定义得到DE为△ABC的中位线,然后根据三角形中位线定理得DE=
BC,
再把DE=3代入计算即可.
| 1 |
| 2 |
再把DE=3代入计算即可.
解答:解:∵OD⊥AB,
∴AD=DB,
∵OE⊥AC,
∴AE=CE,
∴DE为△ABC的中位线,
∴DE=
BC,
∴BC=2DE=2×3=6.
故选A.
∴AD=DB,
∵OE⊥AC,
∴AE=CE,
∴DE为△ABC的中位线,
∴DE=
| 1 |
| 2 |
∴BC=2DE=2×3=6.
故选A.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了三角形中位线定理.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
已知点P(a,-3)和Q(4,b)关于原点对称,则(a+b)2013的值为( )
| A、1 |
| B、-1 |
| C、72013 |
| D、-72013 |
若3<a<4时,化简|a-3|+|a-4|的结果为( )
| A、2a-7 | B、2a-1 |
| C、1 | D、7 |
下列各式中,正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知多项式2x2y|m|-1-
(m+2)y2+3是关于x、y的三次三项式,则m等于( )
| 1 |
| 4 |
| A、±2 | B、2 |
| C、-2 | D、以上都不对 |
 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题: