题目内容
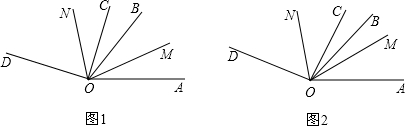 已知∠AOD=α,OB、OC、OM、ON是∠AOD内的射线.
已知∠AOD=α,OB、OC、OM、ON是∠AOD内的射线.
(1)如图1,当α=160°,若OM平分∠AOB,ON平分∠BOD,求∠MON的大小;
(2)如图2,若OM平分∠AOC,ON平分∠BOD,∠BOC=20°,∠MON=60°,求α.
解:(1)∵OM平分∠AOB,ON平分∠BOD,
∴∠BOM= ∠AOB,∠BON=
∠AOB,∠BON= ∠BOD,
∠BOD,
∴∠MON=∠BOM+∠BON= (∠AOB+∠BOD),
(∠AOB+∠BOD),
∵∠AOD=∠AOB+∠BOD=α=160°,
∴∠MON= ×160°=80°;
×160°=80°;
(2)设∠AOB=x,则∠BOD=α-x,
∵OM平分∠AOC,ON平分∠BOD,
∴∠COM= ∠AOC=
∠AOC= (x+20°),∠BON=
(x+20°),∠BON= ∠BOD=
∠BOD= (α-x),
(α-x),
∴∠MON=∠COM+∠BON-∠BOC= (x+20°)+
(x+20°)+ (α-x)-20°=
(α-x)-20°= α-10°,
α-10°,
∵∠MON=60°,
∴ α-10°=60°,
α-10°=60°,
解得α=140°.
分析:(1)根据角平分线的定义求出∠BOM和∠BON,然后根据∠MON=∠BOM+∠BON代入数据进行计算即可得解;
(2)设∠AOB=x,表示出∠BOD=α-x,根据角平分线的定义表示出∠COM和∠BON,然后根据∠MON=∠COM+∠BON-∠BOC列式计算即可得解.
点评:本题考查了角的计算,角平分线的定义,准确识图是解题的关键,难点在于要注意整体思想的利用.
∴∠BOM=
 ∠AOB,∠BON=
∠AOB,∠BON= ∠BOD,
∠BOD,∴∠MON=∠BOM+∠BON=
 (∠AOB+∠BOD),
(∠AOB+∠BOD),∵∠AOD=∠AOB+∠BOD=α=160°,
∴∠MON=
 ×160°=80°;
×160°=80°;(2)设∠AOB=x,则∠BOD=α-x,
∵OM平分∠AOC,ON平分∠BOD,
∴∠COM=
 ∠AOC=
∠AOC= (x+20°),∠BON=
(x+20°),∠BON= ∠BOD=
∠BOD= (α-x),
(α-x),∴∠MON=∠COM+∠BON-∠BOC=
 (x+20°)+
(x+20°)+ (α-x)-20°=
(α-x)-20°= α-10°,
α-10°,∵∠MON=60°,
∴
 α-10°=60°,
α-10°=60°,解得α=140°.
分析:(1)根据角平分线的定义求出∠BOM和∠BON,然后根据∠MON=∠BOM+∠BON代入数据进行计算即可得解;
(2)设∠AOB=x,表示出∠BOD=α-x,根据角平分线的定义表示出∠COM和∠BON,然后根据∠MON=∠COM+∠BON-∠BOC列式计算即可得解.
点评:本题考查了角的计算,角平分线的定义,准确识图是解题的关键,难点在于要注意整体思想的利用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 4、如图,直线AB与CD相交于点O,已知∠AOD=120°,则∠COB的补角是
4、如图,直线AB与CD相交于点O,已知∠AOD=120°,则∠COB的补角是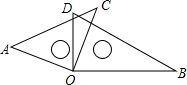 (2011•峨眉山市二模)如图,将一副30°和45°的直角三角板的两个直角叠在一起,使直角顶点重合于点O,已知∠AOD=50°,则∠BOC=
(2011•峨眉山市二模)如图,将一副30°和45°的直角三角板的两个直角叠在一起,使直角顶点重合于点O,已知∠AOD=50°,则∠BOC= (2013•淮北模拟)如图,AB为⊙O直径,点C、D在⊙O上,已知∠AOD=50°,AD∥OC,则∠BOC=
(2013•淮北模拟)如图,AB为⊙O直径,点C、D在⊙O上,已知∠AOD=50°,AD∥OC,则∠BOC=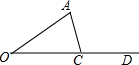 如图,已知∠AOD=30°,点C是射线OD上的一个动点.在点C的运动过程中,△AOC恰好是等腰三角形,则此时∠A所有可能的度数为
如图,已知∠AOD=30°,点C是射线OD上的一个动点.在点C的运动过程中,△AOC恰好是等腰三角形,则此时∠A所有可能的度数为