题目内容
13. 如图,在正方形ABCD中,EB=$\frac{1}{4}$AB,FG⊥ED,EF2=EG•ED,求证:BF=FC.
如图,在正方形ABCD中,EB=$\frac{1}{4}$AB,FG⊥ED,EF2=EG•ED,求证:BF=FC.
分析 由已知条件得到△EGF∽△EFD,于是得到∠EFD=90°,推出△BEF∽△CFD,得到$\frac{BE}{CF}=\frac{BF}{CD}$,即$\frac{\frac{1}{4}AB}{CF}=\frac{AB-CF}{AB}$,得到方程CF2-CF+$\frac{1}{4}$=0,解得CF=$\frac{1}{2}$=$\frac{1}{2}$AB,即可得到结论.
解答 证明:∵EF2=EG•ED,∠E=∠E,
∴△EGF∽△EFD,
∵FG⊥ED,
∴∠EFD=90°,
∴∠BFE=∠CDF=90°-∠DFC,
∵∠B=∠C,
△BEF∽△CFD,
∴$\frac{BE}{CF}=\frac{BF}{CD}$,即$\frac{\frac{1}{4}AB}{CF}=\frac{AB-CF}{AB}$,
设AB=1,
则CF2-CF+$\frac{1}{4}$=0,
解得:CF=$\frac{1}{2}$=$\frac{1}{2}$AB,
∴BF=FC.
点评 本题考查了相似三角形的判定和性质,正方形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
5. 如图,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于F,则图中相似三角形有( )
如图,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于F,则图中相似三角形有( )
 如图,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于F,则图中相似三角形有( )
如图,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于F,则图中相似三角形有( )| A. | 6组 | B. | 5组 | C. | 8组 | D. | 7组 |
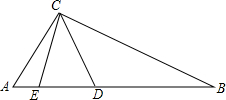 马明和王群在解这样一道题:“如图,在△ABC中,∠ACB=90°,点D、E在边AB上,AD=AC,BE=BC.求∠DCE的度数.”他们经过商量后,结论不一致,马明说:“∠DCE的值与∠B有关,只有告诉∠B的度数才能求出∠DCE的度数.”王群说:“∠DCE的度数是一个定值,与∠B的度数无关.”他们谁说的正确?请说明理由.
马明和王群在解这样一道题:“如图,在△ABC中,∠ACB=90°,点D、E在边AB上,AD=AC,BE=BC.求∠DCE的度数.”他们经过商量后,结论不一致,马明说:“∠DCE的值与∠B有关,只有告诉∠B的度数才能求出∠DCE的度数.”王群说:“∠DCE的度数是一个定值,与∠B的度数无关.”他们谁说的正确?请说明理由. 已知如图,∠BAC=∠BPC,AP平分∠CAN,PN⊥AB于点N,PM⊥AC于M,求$\frac{AC+AB}{CM}$的值.
已知如图,∠BAC=∠BPC,AP平分∠CAN,PN⊥AB于点N,PM⊥AC于M,求$\frac{AC+AB}{CM}$的值.