题目内容
如图，在相距100m的A，B两处观测工厂C，测得∠BAC=60°，∠ABC=45°，则A，B两处到工厂C的距离分别为________和________．
100（
-1）m 50（3
-
）m
分析：过C作CD⊥AB于点D，设CD为x，在Rt△ACD和Rt三角形BCD中，分别用x表示AD、BD，然后根据AB=AD+BD=100求出x的值，继而可求得A，B两处到工厂C的距离．
解答：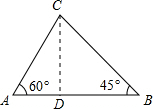
解：过C作CD⊥AB于点D，设CD为x，
在Rt△ACD和Rt△BCD中，
AD=
=
，
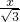BD=x，
则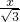+x=100，
解得：x=150-50=50（3-），
又∵
=sin60°，
∴AC=100（-1），
BC=CD=50（3-）．
故答案为：100（-1）m，50（3-）m．
点评：本题考查了解直角三角形的应用，难度适中，解答本题的关键是构造直角三角形并解直角三角形．
-1）m 50（3-）m分析：过C作CD⊥AB于点D，设CD为x，在Rt△ACD和Rt三角形BCD中，分别用x表示AD、BD，然后根据AB=AD+BD=100求出x的值，继而可求得A，B两处到工厂C的距离．
解答：
解：过C作CD⊥AB于点D，设CD为x，在Rt△ACD和Rt△BCD中，
AD=
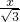=，BD=x，
则
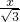+x=100，解得：x=150-50
=50（3-），又∵
=sin60°，∴AC=100（
-1），BC=
CD=50（3-）．故答案为：100（
-1）m，50（3-）m．点评：本题考查了解直角三角形的应用，难度适中，解答本题的关键是构造直角三角形并解直角三角形．
练习册系列答案
相关题目
如图，为了测量河的宽度，王芳同学在河岸边相距200m的M和N两点分别测定对岸一棵树P的位置，P在M的正北方向，在N的北偏西30°的方向，则河的宽度是（ ）A、200
| ||||
B、
| ||||
C、100
| ||||
| D、100m |
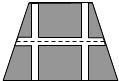如图，要设计一个等腰梯形的花坛，花坛上底长100m，下底长180m，上下底相距80m，在两腰中点连线外有一条横向甬道，上下底之间有两条纵向甬道，各甬道的宽度相等，甬道的面积是梯形面积的六分之一．甬道的宽应是多少（精确到0.01m）？
如图，在相距100m的A，B两处观测工厂C，测得∠BAC=60°，∠ABC=45°，则A，B两处到工厂C的距离分别为
如图，某公园湖亭A在宝塔O的北偏东52°，与点O相距200米，假山B在宝塔O的南偏东38°，与点O相距150米．