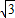题目内容
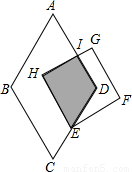
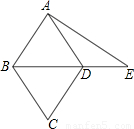
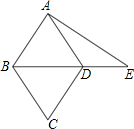如图为菱形ABCD与△ABE的重迭情形，其中D在BE上．若AB=17，BD=16，AE=25，则DE的长度为何？（ ）| A、8 | B、9 | C、11 | D、12 |
分析：首先连接AC，设AC交BD于O点，由四边形ABCD为菱形，利用菱形对角线互相垂直且平分的性质及勾股定理，即可求得DE的长度．
解答：
解：连接AC，设AC交BD于O点，
∵四边形ABCD为菱形，
∴AC⊥BD，且BO=DO=
=8，
在△AOD中，
∵∠AOD=90°，
∴AO=
=
=15，
在△AOE中，
∵∠AOE=90°，
∴OE=
=
=20，
又OD=8，
∴DE=OE-OD=20-8=12．
故选D．
解：连接AC，设AC交BD于O点，∵四边形ABCD为菱形，
∴AC⊥BD，且BO=DO=
| 16 |
| 2 |
在△AOD中，
∵∠AOD=90°，
∴AO=
| AD2-OD2 |
| 172-82 |
在△AOE中，
∵∠AOE=90°，
∴OE=
| AE2-AO2 |
| 252-152 |
又OD=8，
∴DE=OE-OD=20-8=12．
故选D．
点评：此题考查了勾股定理与菱形的性质．解题的关键是注意数形结合思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
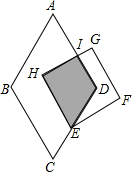如图为菱形ABCD与正方形EFGH的重迭情形，其中E在CD上，AD与GH相交于I点，且AD∥HE．若∠A=60°，且AB=7，DE=4，HE=5，则梯形HEDI的面积为何？（ ）A、6
| ||
B、8
| ||
C、10-2
| ||
D、10+2
|
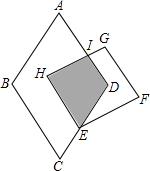如图为菱形ABCD与正方形EFGH的重叠情形，其中E在CD上，AD与GH相交于I点，且AD∥HE．若∠A=60°，且AB=7，DE=4，HE=5，则梯形HEDI的面积为
