题目内容
以下哪些选项可判断二次函数y=ax2+bx+c(a≠0)与x轴有两个交点: (只需填上正确的序号)
①a+b+c=0;②b>a+c;③b=2a+3c;④ac<0.
①a+b+c=0;②b>a+c;③b=2a+3c;④ac<0.
考点:抛物线与x轴的交点
专题:数形结合
分析:当a+b+c=0,即b=-(a+c),再计算△得到△=b2-4ac=(a+c)2-4ac=(a-c)2≥0,因此可判断二次函数y=ax2+bx+c(a≠0)与x轴有一个或两个交点;当b>a+c,不能确定二次函数y=ax2+bx+c(a≠0)与x轴的交点个数;当b=2a+3c或ac<0时,可计算出△>0,于是可判断二次函数y=ax2+bx+c(a≠0)与x轴有两个交点.
解答:解:当a+b+c=0,即b=-(a+c),则△=b2-4ac=(a+c)2-4ac=(a-c)2≥0,所以二次函数y=ax2+bx+c(a≠0)与x轴有一个或两个交点,所以①错误;
当b>a+c,即a-b+c>0,所以当x=-1时,函数值为正数,不能确定二次函数y=ax2+bx+c(a≠0)与x轴的交点个数,所以②错误;
当b=2a+3c,则△=b2-4ac=(2a+3c)2-4ac=4(a+c)2+c2>0,所以二次函数y=ax2+bx+c(a≠0)与x轴有两个交点,所以③正确;
当ac<0,则△=b2-4ac>0,所以二次函数y=ax2+bx+c(a≠0)与x轴有两个交点,所以④正确.
故答案为③④.
当b>a+c,即a-b+c>0,所以当x=-1时,函数值为正数,不能确定二次函数y=ax2+bx+c(a≠0)与x轴的交点个数,所以②错误;
当b=2a+3c,则△=b2-4ac=(2a+3c)2-4ac=4(a+c)2+c2>0,所以二次函数y=ax2+bx+c(a≠0)与x轴有两个交点,所以③正确;
当ac<0,则△=b2-4ac>0,所以二次函数y=ax2+bx+c(a≠0)与x轴有两个交点,所以④正确.
故答案为③④.
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标;二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系,△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
 如图,如果AD∥BC,那么根据
如图,如果AD∥BC,那么根据 如图,直角△DEF是由直角△ABC平移得到的,如果AB=6cm,CF=5cm,DG=2cm,那么图中阴影部分四边形DGCF的面积是
如图,直角△DEF是由直角△ABC平移得到的,如果AB=6cm,CF=5cm,DG=2cm,那么图中阴影部分四边形DGCF的面积是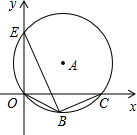 如图,点E,O,C在半径为5的⊙A上,BE是⊙A上的一条弦,cos∠OBE=
如图,点E,O,C在半径为5的⊙A上,BE是⊙A上的一条弦,cos∠OBE=