题目内容
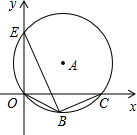 如图,点E,O,C在半径为5的⊙A上,BE是⊙A上的一条弦,cos∠OBE=
如图,点E,O,C在半径为5的⊙A上,BE是⊙A上的一条弦,cos∠OBE=| 4 |
| 5 |
考点:垂径定理,坐标与图形性质,圆周角定理,解直角三角形
专题:
分析:过点O作OH⊥BE,垂足为H,连接AC.证得∠OBE=∠ECO,结合90度的圆周角所对的弦是直径,求得EO的长度,然后结合三角函数求得EB的长度,再用勾股定理求得BC的长度.
解答: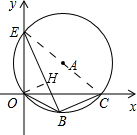 解:过点O作OH⊥BE,垂足为H,连接AC.
解:过点O作OH⊥BE,垂足为H,连接AC.
因为∠OBE=∠ECO,
∴cos∠OBE=cos∠OCE=
,
又∵∠EOC=90°,所以EC是⊙O的直径,半径为5,
所以cos∠OCE=
=
,
∴OC=8.
由勾股定理得:EO=6,
又∵∠OEB=30°
∴OH=3,EH=3
,
∵∠OEB=30°,
∴∵∠OAB=30°,
∴△OAB是等边三角形,
所以OA=OB=AB=5,
根据勾股定理,BH=4,
所以EB=3
+4,∴BC2=EC2-EB2=100-(3
+4)2=(4
-3)2,
所BC=4
-3.
故答案为:4
-3.
 解:过点O作OH⊥BE,垂足为H,连接AC.
解:过点O作OH⊥BE,垂足为H,连接AC.因为∠OBE=∠ECO,
∴cos∠OBE=cos∠OCE=
| 4 |
| 5 |
又∵∠EOC=90°,所以EC是⊙O的直径,半径为5,
所以cos∠OCE=
| OC |
| EC |
| 4 |
| 5 |
∴OC=8.
由勾股定理得:EO=6,
又∵∠OEB=30°
∴OH=3,EH=3
| 3 |
∵∠OEB=30°,
∴∵∠OAB=30°,
∴△OAB是等边三角形,
所以OA=OB=AB=5,
根据勾股定理,BH=4,
所以EB=3
| 3 |
| 3 |
| 3 |
所BC=4
| 3 |
故答案为:4
| 3 |
点评:本题主要考查了90度的圆周角所对的弦是直径这一性质的应用,解答本题的关键在于如何构造直角三角形结合三角函数求出线段的长度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
化简
的结果是( )
| -a3b2c |
| ab |
| A、-a2b |
| B、-a2c |
| C、-a2bc |
| D、-bc |
 如图,AB∥CD,∠A=40°,∠C=65°,则∠E=
如图,AB∥CD,∠A=40°,∠C=65°,则∠E=