题目内容
某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元, 如果平均每月
增长率为x,则由题意列方程为( )
A.200(1+x)2=1000
B.200+200×2x=1000
C.200+200×3x=1000
D.200[1+(1+x)+(1+x)2]=1000
D
【解析】
试题分析:先得到二月份的营业额,三月份的营业额,等量关系为:一月份的营业额+二月份的营业额+三月份的营业额=1000万元,把相关数值代入即可.
∵一月份的营业额为200万元,平均每月增长率为x,
∴二月份的营业额为200×(1+x),
∴三月份的营业额为200×(1+x)×(1+x)=200×(1+x)2,
∴可列方程为200+200×(1+x)+200×(1+x)2=1000,
即200[1+(1+x)+(1+x)2]=1000.
故选D
考点:由实际问题抽象出一元二次方程
考点分析: 考点1:一元二次方程 定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:

它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中 ax2叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
(10分)张明、王成两位同学初二一学年10次数学单元自我检测的成绩(成绩均为整数,且个位数为0)分别如下图所示:利用图中提供的信息,解答下列问题.
(1)完成下表
姓名 | 平均成绩 | 中位数 | 众数 | 方差(S2) |
张明 | 80 | 80 | ||
王成 | 260 |
(2)如果将90分以上(含90分)的成绩视为A等,则获得成绩为A等多的同学是 ;
(3)根据图表信息,请你对这位两同学各提一条不超过20个字的学习建议,并说明提出建议的原因.

 的一元二次方程
的一元二次方程 的一个根是1,则
的一个根是1,则 = .
= . 有两个不相等的实数根,则k的取值范围是 .
有两个不相等的实数根,则k的取值范围是 . ,应如何设计每个彩条的宽度?
,应如何设计每个彩条的宽度?
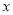 的一元二次方程
的一元二次方程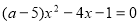 有实数根,则
有实数根,则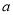 满足条件是( )
满足条件是( )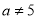 B、
B、 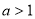 且
且 C、.
C、. 且
且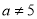 D、
D、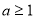
 的解为 .
的解为 .