题目内容
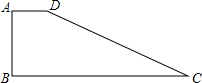直角梯形ABCD，AD∥BC，∠B=90°，且腰AB=5，两底差为12，则另一腰CD=________．
13
分析：过点D作DE⊥BC于E，先求出四边形ABED是矩形，根据矩形的对边相等可得DE=AB，BE=AD，再求出CE，然后利用勾股定理列式进行计算即可得解．
解答：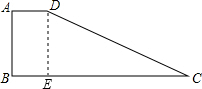
解：如图，过点D作DE⊥BC于E，
∵AD∥BC，∠B=90°，
∴AB∥DE，
∴四边形ABED是矩形，
∴DE=AB，BE=AD，
∵腰AB=5，两底差为12，
∴DE=5，CE=12，
根据勾股定理，CD=
=
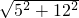=13．
故答案为：13．
点评：本题考查了直角梯形的性质，矩形的判定与性质，勾股定理的应用，作辅助线把直角梯形分成一个矩形与一个直角三角形是解题的关键．
分析：过点D作DE⊥BC于E，先求出四边形ABED是矩形，根据矩形的对边相等可得DE=AB，BE=AD，再求出CE，然后利用勾股定理列式进行计算即可得解．
解答：
解：如图，过点D作DE⊥BC于E，∵AD∥BC，∠B=90°，
∴AB∥DE，
∴四边形ABED是矩形，
∴DE=AB，BE=AD，
∵腰AB=5，两底差为12，
∴DE=5，CE=12，
根据勾股定理，CD=
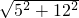==13．故答案为：13．
点评：本题考查了直角梯形的性质，矩形的判定与性质，勾股定理的应用，作辅助线把直角梯形分成一个矩形与一个直角三角形是解题的关键．
练习册系列答案
相关题目
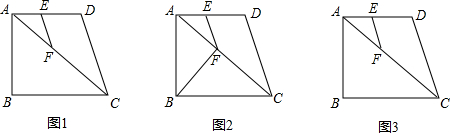
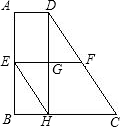如图，在直角梯形ABCD中，AD∥BC，AB⊥BC，AD=1，BC=3，CD=4．梯形的高DH与中位线EF交于点G，则下列结论中：
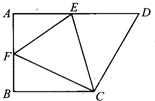12、如图，在直角梯形ABCD中，AD∥BC，∠B=90°，将直角梯形ABCD沿CE折叠，使点D落在AB上的F点，若AB=BC=12，EF=10，∠FCD=90°，则AF=
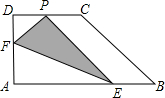如图，直角梯形纸片ABCD，AD⊥AB，AB=6，AD=CD=3，点E、F分别在线段AB、AD上，将△AEF沿EF翻折，点A的落点记为P．当P落在直角梯形ABCD内部时，PD的最小值等于
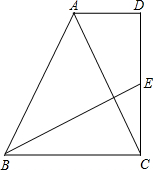如图所示，在直角梯形ABCD中，∠BCD=90°，AD∥BC，CD=BC，E是CD上一点，BE⊥AC．