题目内容
7．
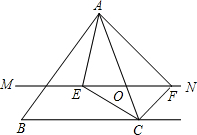如图，在△ABC中，点O是AC边上的一个动点，过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．（1）求证：OE=OF；
（2）当点O是AC的中点，△ABC进行怎样的变化才能使四边形AECF是正方形？
分析 （1）根据角平分线定义得∠1=∠2，再根据平行线的性质得∠1=∠3，则∠2=∠3，所以OE=OC，同理可得OC=OF，所以OE=OF；
（2）由OE=OF，OA=OC可判断四边形AECF为平行四边形，再证明∠ECF=90°，则可判断四边形AECF为矩形，根据正方形的判定方法，当∠2=45°时，四边形AECF为正方形，于是可得∠ACB=90°．
解答 （1）证明：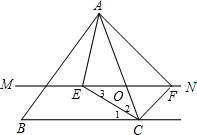
如图，
∵CE平分∠BCA，
∴∠1=∠2，
∵MN∥BC，
∴∠1=∠3，
∴∠2=∠3，
∴OE=OC，
同理可得OC=OF，
∴OE=OF；
（2）解：∵OE=OF，OA=OC，
∴四边形AECF为平行四边形，
∵CE平分∠ACB，CF平分∠ACB的外角，
∴∠ECF=90°，
∴四边形AECF为矩形，
当∠2=45°时，四边形AECF为正方形，
此时∠ACB=90°，
即当点O是AC的中点，△ABC中∠ACB=90°时，四边形AECF是正方形．
点评 本题考查了正方形的判定：先判定四边形是矩形，再判定这个矩形有一组邻边相等；先判定四边形是菱形，再判定这个菱形有一个角为直角．
练习册系列答案
相关题目
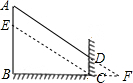如图，一位同学想利用影子测量旗杆的高度，在同一时刻，测得一米长的标杆的影长为1.2米，但他测旗杆影子时，因旗杆靠近教室，影子的一部分落在了墙上．他先测得地面部分的影子长为12米，又测得墙上影高为2米，求旗杆的高度AB．
16．根式$\sqrt{\frac{1}{2}x-\sqrt{3}}$中x的取值范围是（ ）
| A． | x＞2$\sqrt{3}$ | B． | x＜2$\sqrt{3}$ | C． | x≥2$\sqrt{3}$ | D． | x≤2$\sqrt{3}$ |
