题目内容
1.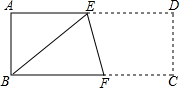 已知,如图长方形ABCD中,AB=6cm,AD=12cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
已知,如图长方形ABCD中,AB=6cm,AD=12cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )| A. | $\frac{9}{2}$cm2 | B. | 6cm2 | C. | $\frac{27}{2}$cm2 | D. | 18cm2 |
分析 根据翻折的性质可得BE=DE,设AE=x,表示出BE,在Rt△ABE中,利用勾股定理列方程求出x的值,再根据三角形的面积公式列式计算即可得解.
解答 解:∵长方形折叠,使点B与点D重合,
∴BE=DE,
设AE=x,则BE=DE=12-x,
在Rt△ABE中,根据勾股定理得,AB2+AE2=BE2,
即62+x2=(12-x)2,
解得x=$\frac{9}{2}$,
所以,△ABE的面积=$\frac{1}{2}$AB•AE=$\frac{1}{2}$×6×$\frac{9}{2}$=$\frac{27}{2}$cm2.
故选C.
点评 本题考查了翻折变换的性质,矩形的性质,勾股定理,此类题目,利用勾股定理列方程求出相关线段的长度的解题的关键.

练习册系列答案
相关题目
12. 如图,二次函数y=ax2+bx+c的图象经过点(1,1)和点(3,0).下列关于这个二次函数的描述,正确的是( )
如图,二次函数y=ax2+bx+c的图象经过点(1,1)和点(3,0).下列关于这个二次函数的描述,正确的是( )
 如图,二次函数y=ax2+bx+c的图象经过点(1,1)和点(3,0).下列关于这个二次函数的描述,正确的是( )
如图,二次函数y=ax2+bx+c的图象经过点(1,1)和点(3,0).下列关于这个二次函数的描述,正确的是( )| A. | y的最大值大于1 | B. | 当x=0时,y的值大于0 | ||
| C. | 当x=2时,y的值等于1 | D. | 当x>3时,y的值大于0 |
9.一幅平面图的比例尺是10:1,实际距离1厘米在这幅图上应画( )
| A. | 1毫米 | B. | 1厘米 | C. | 1分米 | D. | 10分米 |
6.若|a-2|+(b+3)2=0,则(a+b)2008的值是( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2008 |
13.在下面的四个几何体中,左视图与主视图不完全相同的几何是( )
| A. |  正方体 | B. |  长方体 | C. |  球 | D. |  圆锥 |
10.在0,2,3,(-5)0这四个数中,最大的数是( )
| A. | 0 | B. | 2 | C. | 3 | D. | (-5)0 |
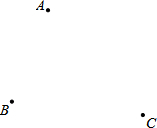 如图,平面上有三个点A,B,C,利用尺规按要求作图;
如图,平面上有三个点A,B,C,利用尺规按要求作图;