题目内容
 如图,已知∠1=∠2,∠B=∠C,小丽在图上把两组相等角的信息标注出来后,略加分析,便发现CE∥BF.同桌的小聪说:“我还能得到∠A=∠D呢.”小丽深入思考后,很快也明白了小聪是怎么得到∠A=∠D的了.你能写出得到CE∥BF,∠A=∠D的过程吗?
如图,已知∠1=∠2,∠B=∠C,小丽在图上把两组相等角的信息标注出来后,略加分析,便发现CE∥BF.同桌的小聪说:“我还能得到∠A=∠D呢.”小丽深入思考后,很快也明白了小聪是怎么得到∠A=∠D的了.你能写出得到CE∥BF,∠A=∠D的过程吗?考点:平行线的判定与性质
专题:
分析:由∠1=∠2结合对顶角相等可证明CE∥BF,进一步可得到∠C+∠CEB=180°,可证明AB∥CD,可得到∠A=∠D.
解答:证明:
∵∠1=∠2,且∠1=∠3,
∴∠2=∠3,
∴CE∥BF,
∴∠B+∠CEB=180°,
又∠B=∠C,
∴∠C+∠CEB=180°,
∴AB∥CD,
∴∠A=∠D.
∵∠1=∠2,且∠1=∠3,
∴∠2=∠3,
∴CE∥BF,
∴∠B+∠CEB=180°,
又∠B=∠C,
∴∠C+∠CEB=180°,
∴AB∥CD,
∴∠A=∠D.
点评:本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c?a∥c.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图是一个上下底密封纸盒(底面为正六边形)的三视图,请你根据图中数据,计算这个密封纸盒的表面积为
如图是一个上下底密封纸盒(底面为正六边形)的三视图,请你根据图中数据,计算这个密封纸盒的表面积为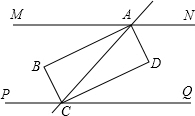 已知MN∥PQ,AB,BC分别平分∠MAC,∠PCA,交于点B,AD,DC分别平分∠NAC,∠QCA,交于点D.求证:四边形ABCD是矩形.
已知MN∥PQ,AB,BC分别平分∠MAC,∠PCA,交于点B,AD,DC分别平分∠NAC,∠QCA,交于点D.求证:四边形ABCD是矩形. 如图所示,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,它的左视图是( )
如图所示,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,它的左视图是( )



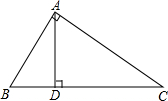 在△ABC中,∠BAC=90°,AD⊥BC于点D,若AB=30cm,BC=50cm,求线段CD的长.
在△ABC中,∠BAC=90°,AD⊥BC于点D,若AB=30cm,BC=50cm,求线段CD的长.