题目内容
已知,如图,在平行四边形ABCD中,∠ABC的平分线与AD相交于点P,下列说法中正确的是（ ）
①△APB是等腰三角形 ②∠ABP+∠BPD=180°③PD+CD=BC
④
A. ①②④ B. ①②③ C. ①③④ D. ①②③④
【答案】
B．
【解析】
试题分析：∵在平行四边形ABCD中,∠ABC的平分线与AD相交于点P,
∴∠ABP=∠CBP=∠APB,所以△APB是等腰三角形,①正确；
∵四边形ABCD是平行四边形,
∴∠ABP+∠BPD=180°
∵∠ABP=∠CBP
∴∠CBP+∠BPD=180°,②正确；
∵△APB是等腰三角形
∴AP=AB=CD
∵AP+PD=AD=BC
∴PD+CD=BC, ③正确；
∵
与
高相等,要使得
,则必须满足PD+BC=2AP,从题目中无法得知,
∴④错误.
故选B．
考点：平行四边形性质．
练习册系列答案
相关题目
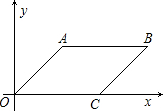如图，在平行四边形ABC0中，已知点A、C两点的坐标为A（
（2013•南平模拟）如图，已知四边形ABCD．请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形ABCD是平行四边形，并予证明．
如图，在平行四边形OABC中，已知点A、C两点的坐标为A （
3，
，将∠OBA对折，使点O的对应点H恰好落在直线AB上，折痕交x轴于点C，