如图.把两个边长相等的等边△ABC和△ACD拼成菱形ABCD.点E.F分别是射线CB.DC上的动点.且始终保持BE=CF.连结AE.AF.EF．(1)求证:①△ABE≌△ACF,②△AEF是等边三角形,(2)①当点E运动到什么位置时.EF⊥DC?②若AB=4.当∠EAB=15°时.求△CEF的面积． (1)①证明见解析,②证明见解析, (2)①当E运动到BE 题目和参考答案——青夏教育精英家教网——

题目内容

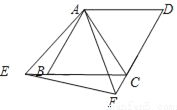
如图，把两个边长相等的等边△ABC和△ACD拼成菱形ABCD，点E、F分别是射线CB、DC上的动点（E、F与B、C、D不重合），且始终保持BE=CF，连结AE、AF、EF．

（1）求证：①△ABE≌△ACF；②△AEF是等边三角形；

（2）①当点E运动到什么位置时，EF⊥DC？

②若AB=4，当∠EAB=15°时，求△CEF的面积．

（1）①证明见解析；②证明见解析；（2）①当E运动到BE=BC时，EF⊥DC； ②△CEF的面积为．【解析】试题分析：（1）①由等边三角形的性质即可得出∠ABE=∠ACF，即可得出结论； ②由全等三角形的性质即可得出结论；（2）①由直角三角形的性质求出和即可得出结论； ②先求出再用勾股定理求出再判断出即可求出最后用三角形的面积公式即可得出结论．试题解析：（1...

练习册系列答案

伴你学江苏系列答案

启航新课堂系列答案

随堂小考系列答案

成才之路高中新课程学习指导系列答案

同步轻松练习系列答案

课课通课程标准思维方法与能力训练系列答案

钟书金牌教材金练系列答案

名牌学校分层课课练系列答案

培优夺冠王系列答案

百分百夺冠卷系列答案

相关题目

将如图所示的正方体的展开图重新折叠成正方体后，和“应”字相对面上的汉字是_____．

静【解析】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．【解析】正方体的表面展开图，相对的面之间一定相隔一个正方形， “沉”与“考”相对，“着”与“冷”相对，“应”与“静”相对．故答案为：静．

如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC，则AM平分∠DAB吗？试说明理由。（提示：过点M作ME垂直AD于E）。

见解析【解析】试题分析：过M作ME⊥AD，根据DM平分∠ADC得到∠1=∠2，根据角平分线的性质得出ME=MC，根据中点得出MC=MB，则ME=MB，然后根据角平分线的逆定理得出答案．试题解析：AM平分∠DAB 理由：过点M作ME⊥AD，垂足为E， ∵DM平分∠ADC， ∴∠1=∠2， ∵MC⊥CD，ME⊥AD， ∴ME=MC（角平分线上的点到角两边的距离相等）， ...

如图，已知DE∥BC， AB∥CD，E为AB的中点，∠A=∠B．下列结论：①CD=AE；②AC=DE；③AC平分∠BCD；④O点是DE的中点；⑤AC=AB．其中正确的是（　　）

A. ①②④ B. ①③⑤ C. ②③④ D. ②④⑤

A 【解析】试题分析：∵已知DE∥BC，AB∥CD，∴四边形BCDE为平行四边形，∴CB=DE； ∵∠A=∠B，∴AC=BC， ∴AC=DE，即可得②正确；根据平行线等分线段性质可得AO=CO，∵AB∥CD，∴∠A=∠DCO，又∵∠AOE=∠COD， ∴△AOE≌△COD（ASA）， ∴AE=CD，即可得①正确； OE=OD，O点是DE的中点；即可得④正确；结论③...

已知点P(－2，1)，那么点P关于x轴对称的点P′的坐标是（）

A. (－2，1) B. (－2，－1) C. (－1，2) D. (2，1)

B 【解析】试题分析：点的坐标关于x轴对称，则对称点坐标也关于x轴对称，横坐标不变，纵坐标变为相反数。故P 坐标为（-2，-1），选B.

如图，将矩形纸片ABCD沿AE折叠，使点B落在对角线AC上的点F处，再沿EG折叠，使点C落在矩形内的点H处，且E、F、H在同一直线上，若AB=6，BC=8，则CG的长是_____．

【解析】试题解析：设BE=x，则EF=x，CE=8?x，由折叠可得，AF=AB=6，由勾股定理,可得 ∴CF=10?6=4，在中,由勾股定理可得, 解得x=3, ∴BE=3，CE=5，由折叠可得, 又又 ∴ 即故答案为：

如图，Rt△ABC的锐角顶点A、B分别在直线EF、GH上，且EF∥GH，若∠CAF=65°，则∠CBH的度数为（　　）

A. 20° B. 25° C. 30° D. 35°

B 【解析】试题解析：∵, 中, 故选B.

计算：（x+y）2﹣（x﹣y）（x+y）

2xy+2y2 【解析】试题分析:利用完全平方公式和平方差公式进行计算,然后再合并同类项即可求解. 试题解析:（x+y）2﹣（x﹣y）（x+y） =x2+2xy+y2﹣（x2﹣y2） =2xy+2y2

一只跳蚤在第一象限及x轴、y轴上跳动，在第一秒钟，它从原点跳动到（0，1），然后接着按图中箭头所示方向跳动[即（0，0）→（0，1）→（1，1）→（1，0）→…]，且每秒跳动一个单位，那么第35秒时跳蚤所在位置的坐标是（）

A. （4，0） B. （5，0） C. （0，5） D. （5，5）

B 【解析】试题分析：由题目中所给的质点运动的特点找出规律，即可解答．【解析】跳蚤运动的速度是每秒运动一个单位长度，（0，0）→（0，1）→（1，1）→（1，0）用的秒数分别是1秒，2秒，3秒，到（2，0）用4秒，到（2，2）用6秒，到（0，2）用8秒，到（0，3）用9秒，到（3，3）用12秒，到（4，0）用16秒，依此类推，到（5，0）用35秒．故第35秒时跳蚤所在位置...