题目内容
解方程
(1) x2-4x+2=0
(2)3(x+2)2=x(x+2)
(3)
(1) ,
, ;(2)x1=-2,x2=-3;(3)x1=-1,x2=-3。
;(2)x1=-2,x2=-3;(3)x1=-1,x2=-3。
【解析】
试题分析:(1)把原方程的常数项2移到方程的右边,方程两边都加上一次项系数一半的平方进行配方,再开平方得到两个一元一次方程,求解即可;
(2)方程移项,两边提取公因式(x+2),可得到两个一元一次方程,求解即可;
(3)把(x-1)看成一个整体,再进行因式分解,到两个一元一次方程,求解即可.
试题解析:(1)∵x2-4x+2=0
∴x2-4x=-2
x2-4x+4=-2+4
(x-2)2=2
∴x-2=
解得: ,
, ;
;
(2)∵3(x+2)2=x(x+2)
∴3(x+2)2-x(x+2)=0
(x+2)(2x+6)=0
∴x+2=0,2x+6=0
解得:x1=-2,x2=-3;
(3)∵
∴[(x-1)+2][(x-1)+4]=0
∴x+1=0,x+3=0
解得:x1=-1,x2=-3.
考点:1.解一元二次方程---配方法;1.解一元二次方程---因式分解法.

练习册系列答案
相关题目


 有两个不相等的实数根,那么
有两个不相等的实数根,那么 的取值范围是
的取值范围是 >
> B.
B. 且
且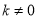
 D.
D. ≥
≥ 且
且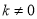

 ,把△EFO缩小,则点E的对应点E′的坐标是( )
,把△EFO缩小,则点E的对应点E′的坐标是( ) +
+ =0,则
=0,则 .
. 这几个有理数中,负数的个数是( )
这几个有理数中,负数的个数是( )