题目内容
在△ABC中,∠A=80°,∠ABC与∠ACB的平分线交于点O,
(1)求∠BOC的度数;
(2)若将∠A换个度数,得到的∠BOC的度数是多少?找出∠A和∠BOC之间的数量关系.
(1)求∠BOC的度数;
(2)若将∠A换个度数,得到的∠BOC的度数是多少?找出∠A和∠BOC之间的数量关系.
考点:三角形内角和定理
专题:
分析:(1)根据三角形的内角和定理求出∠ABC+∠ACB,再根据角平分线的定义求出∠OBC+∠OCB,然后利用三角形的内角和定理列式计算即可得解;
(2)思路同(1)求解即可.
(2)思路同(1)求解即可.
解答: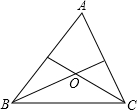 解:(1)∵∠A=80°,
解:(1)∵∠A=80°,
∴∠ABC+∠ACB=180°-80°=100°,
∵∠ABC与∠ACB的平分线交于点O,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
×100°=50°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-50°=130°;
(2)∵∠ABC与∠ACB的平分线交于点O,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
(180°-∠A),
∴∠BOC=180°-(∠OBC+∠OCB)=180°-
(180°-∠A)=90°+
∠A,
即∠BOC=90°+
∠A.
 解:(1)∵∠A=80°,
解:(1)∵∠A=80°,∴∠ABC+∠ACB=180°-80°=100°,
∵∠ABC与∠ACB的平分线交于点O,
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=180°-50°=130°;
(2)∵∠ABC与∠ACB的平分线交于点O,
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=180°-
| 1 |
| 2 |
| 1 |
| 2 |
即∠BOC=90°+
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键,作出图形更形象直观.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
计算(
)2013×1.52012×(-1)2014的结果是( )
| 2 |
| 3 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
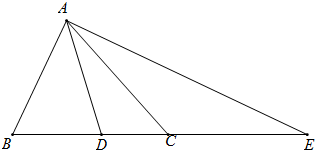 的度数.
的度数.