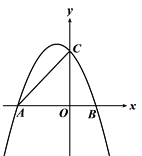题目内容
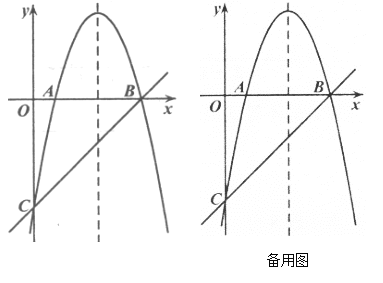
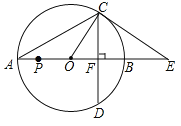
【题目】抛物线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与
,与![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() 且
且![]() .
.
(1)求抛物线的解析式;
(2)点![]() 是
是![]() 轴上一点,当
轴上一点,当![]() 和
和![]() 相似时,求点
相似时,求点![]() 的坐标.
的坐标.
【答案】(1)y=![]() x2-
x2-![]() x+2(2)(0,
x+2(2)(0,![]() )或(0,-
)或(0,-![]() )
)
【解析】
(1)由题意得抛物线的对称轴为x=![]() ,再求出A点坐标,由
,再求出A点坐标,由![]() ,进而求出OC的长,即可求解;
,进而求出OC的长,即可求解;
(2)由△BOC∽△COA,得∠OCB=∠OAC,当![]() 和
和![]() 相似时,分两种情况:①
相似时,分两种情况:①![]() ,②
,②![]() ,分别求出符合题意的OP的长,即可得到P点坐标
,分别求出符合题意的OP的长,即可得到P点坐标
解:(1)由题意得抛物线的对称轴为x=![]() ,
,
∵点![]() 和点
和点![]() 关于对称轴对称,∴A(4,0)
关于对称轴对称,∴A(4,0)
∵![]() =4×1=4,
=4×1=4,
∴OC=2,
∴C(0,2)
∴![]()
解得:m=![]() ,n=2
,n=2
∴解析式为y=![]() x2-
x2-![]() x+2
x+2
(2)由题意,可得AB=3,BC=![]() ,AC=2
,AC=2![]() ,
,
∵![]() ,
,
∴![]() ,又∠BOC=∠COA
,又∠BOC=∠COA
∴△BOC∽△COA,
∴∠OCB=∠OAC,
∴当![]() 和
和![]() 相似时,分两种情况:
相似时,分两种情况:
①![]() 时,得
时,得![]() ,解得CP=
,解得CP=![]()
∴OP=OC-CP=2-![]() =
=![]()
∴P(0,![]() );
);
②![]() ,得
,得![]() ,解得CP=
,解得CP=![]()
∴OP=CP-OC=![]() -2=
-2=![]()
∴P(0,-![]() );
);
综上可得P的坐标为(0,![]() )或(0,-
)或(0,-![]() ).
).

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目