题目内容
 如图,当圆形桥孔中的水面宽度AB为8米时,弧ACB恰为半圆.当水面上涨1米时,桥孔中的水面宽度A′B′为
如图,当圆形桥孔中的水面宽度AB为8米时,弧ACB恰为半圆.当水面上涨1米时,桥孔中的水面宽度A′B′为
- A.
 米
米 - B.
 米
米 - C.
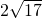 米
米 - D.不能计算
B
分析:根据勾股定理和垂径定理即可得.
解答: 解:设圆的圆心是O,作弦A′B′的弦心距OE,连接OA′.
解:设圆的圆心是O,作弦A′B′的弦心距OE,连接OA′.
根据题意,得在直角三角形OA′E中,OA′=4,OE=1.
根据勾股定理得A′E= m.
m.
再根据垂径定理得A′B′=2A′E=2 m.
m.
故选B.
点评:此类题中常见的辅助线是作弦的弦心距,综合运用勾股定理和垂径定理进行计算.
分析:根据勾股定理和垂径定理即可得.
解答:
 解:设圆的圆心是O,作弦A′B′的弦心距OE,连接OA′.
解:设圆的圆心是O,作弦A′B′的弦心距OE,连接OA′.根据题意,得在直角三角形OA′E中,OA′=4,OE=1.
根据勾股定理得A′E=
 m.
m.再根据垂径定理得A′B′=2A′E=2
 m.
m.故选B.
点评:此类题中常见的辅助线是作弦的弦心距,综合运用勾股定理和垂径定理进行计算.

练习册系列答案
相关题目
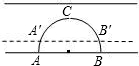 如图,当圆形桥孔中的水面宽度AB为8米时,弧ACB恰为半圆.当水面上涨1米时,桥孔中的水面宽度A′B′为( )
如图,当圆形桥孔中的水面宽度AB为8米时,弧ACB恰为半圆.当水面上涨1米时,桥孔中的水面宽度A′B′为( )A、
| ||
B、2
| ||
C、2
| ||
| D、不能计算 |

 米
米 米
米 米
米
 米
米 米
米 米
米
 米
米 米
米 米
米