题目内容
【题目】如图1,抛物线 ![]() 经过
经过 ![]() ,
, ![]() 两点,与
两点,与 ![]() 轴相交于点
轴相交于点 ![]() ,连接
,连接 ![]() .点
.点 ![]() 为抛物线上一动点,过点
为抛物线上一动点,过点 ![]() 作
作 ![]() 轴的垂线
轴的垂线 ![]() ,交直线
,交直线 ![]() 于点
于点 ![]() ,交
,交 ![]() 轴于点
轴于点 ![]() .
.
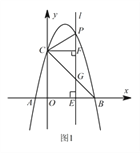
Ⅰ 求抛物线的表达式;
Ⅱ 当 ![]() 位于
位于 ![]() 轴右边的抛物线上运动时,过点
轴右边的抛物线上运动时,过点 ![]() 作
作 ![]() 直线
直线 ![]() ,
, ![]() 为垂足.当点
为垂足.当点 ![]() 运动到何处时,以
运动到何处时,以 ![]() ,
, ![]() ,
, ![]() 为顶点的三角形与
为顶点的三角形与 ![]() 相似?并求出此时点
相似?并求出此时点 ![]() 的坐标;
的坐标;
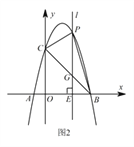
Ⅲ 如图2,当点 ![]() 在位于直线
在位于直线 ![]() 上方的抛物线上运动时,连接
上方的抛物线上运动时,连接 ![]() ,
, ![]() .请问
.请问 ![]() 的面积
的面积 ![]() 能否取得最大值?若能,请求出最大面积
能否取得最大值?若能,请求出最大面积 ![]() ,并求出此时点
,并求出此时点 ![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
【答案】(1)抛物线的表达式为 ![]() ;(2)点
;(2)点 ![]() 的坐标为
的坐标为 ![]() 或
或 ![]() ;(3)当
;(3)当 ![]() 时,
时, ![]() 的面积
的面积 ![]() 能取最大值
能取最大值 ![]() ,此时
,此时 ![]() 点坐标为
点坐标为 ![]() .
.
【解析】(1) 由题意得: ![]()
解得 ![]()
![]() 抛物线的表达式为
抛物线的表达式为 ![]() .
.
(2) ![]() 点坐标为
点坐标为 ![]() ,
,
![]()
![]() 为等腰直角三角形,且
为等腰直角三角形,且 ![]() 为直角.
为直角.
![]()
![]() ,
, ![]() ,
, ![]() 为顶点的三角形与
为顶点的三角形与 ![]() 相似,
相似,
![]()
![]()
又 ![]() 直线
直线 ![]() ,
,
![]()
![]() .
.
设 ![]() ,则
,则 ![]() ,
,
![]() .
.
![]()
![]() ,
,
![]()
![]() ,解得
,解得 ![]() 或
或 ![]() .
.
![]() 点
点 ![]() 的坐标为
的坐标为 ![]() 或
或 ![]() .
.
(3) ![]()
![]() ,
, ![]() ,
,
![]() 直线
直线 ![]() 的表达式为
的表达式为 ![]() ,
,
设 ![]() ,则
,则 ![]() ,
,
![]()
![]() .
.
![]()
![]() .
.
![]() 当
当 ![]() 时,
时, ![]() 的面积
的面积 ![]() 能取最大值
能取最大值 ![]() ,此时
,此时 ![]() 点坐标为
点坐标为 ![]() .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
