Question

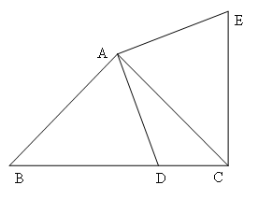
【题目】如图，甲、乙为两座建筑物，它们之间的水平距离BC为30日，在A点测得D点的仰角∠EAD=45°，在B点测得D点的仰角为∠CBD=60°，测得甲、乙这两座建筑物的高度分别为（　　）米．

A. 10，30 B. 30，30 C. 30﹣3，30 D. 30﹣30，30

Answer 1

【答案】D

【解析】

在Rt△BCD中可求得CD的长，即求得乙的高度，延长AE交CD于F，则AF∥BC，求得∠AFD＝90°，在Rt△ADF中可求得DF，则可求得CF的长，即可求得甲的高度．

延长AE交CD于F，则AF∥BC，

∵AB⊥BC，DC⊥BC，

∴AF⊥DC，

∴∠AFD＝∠AFC＝∠ABC＝∠BCD＝90°．

∴四边形ABCF为矩形，

∴AF＝BC＝30m，FC＝AB．

∵∠DAE＝45°，

∴∠ADF＝45°，

∴DF＝AF＝30m，

在Rt△BCD中，DC＝BCtan∠DBC＝30，

∴FC＝DCDF＝3030，

答：甲建筑物的高AB为（3030）m，乙建筑物的高DC为30m．

故选：D．