题目内容
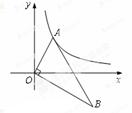
如图,过点O作直线与双曲线y= (k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是( )
(k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是( )

A.S1=S2 B.2S1=S2 C.3S1=S2 D.4S1=S2
 (k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是( )
(k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是( )
A.S1=S2 B.2S1=S2 C.3S1=S2 D.4S1=S2
B
试题分析:设A点坐标为(m,n),
过点O的直线与双曲线y=
 交于A、B两点,则A、B两点关与原点对称,则B的坐标为(﹣m,﹣n);
交于A、B两点,则A、B两点关与原点对称,则B的坐标为(﹣m,﹣n);矩形OCBD中,易得OD=﹣n,OC=m;则S1=﹣mn;
在Rt△EOF中,AE=AF,故A为EF中点,
由中位线的性质可得OF=﹣2n,OE=2m;
则S2=
 OF×OE=﹣2mn;
OF×OE=﹣2mn;故2S1=S2.
故选B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 轴,
轴,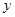 轴上,点D在第一象限内,DC⊥
轴上,点D在第一象限内,DC⊥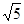 ,反比例函数
,反比例函数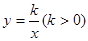 的图象过CD的中点E。
的图象过CD的中点E。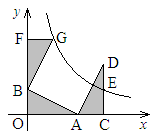
 的值;
的值; 中,正方形
中,正方形 的边长为2.写出一个函数
的边长为2.写出一个函数 ,使它的图象与正方形
,使它的图象与正方形
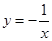 的图象上有两点
的图象上有两点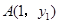 ,
,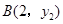 ,则
,则 ______
______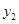 (填“
(填“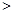 ”或“
”或“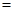 ”或“
”或“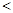 ”).
”). (k≠0)上,将正方形沿x轴负方向平移 m个单位长度后,点C恰好落在双曲线上,则m的值是 ( )
(k≠0)上,将正方形沿x轴负方向平移 m个单位长度后,点C恰好落在双曲线上,则m的值是 ( )


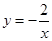 上有两点A(x1,y1)、B(x2,y2),若y1>y2,则x1-x2的值是( )
上有两点A(x1,y1)、B(x2,y2),若y1>y2,则x1-x2的值是( )