题目内容
 20、如图,已知∠EFD=∠BCA,BC=EF,AF=DC.则AB=DE.请说明理由.(填空)
20、如图,已知∠EFD=∠BCA,BC=EF,AF=DC.则AB=DE.请说明理由.(填空)解:∵AF=DC(已知)
∴AF+
FC
=DC+CF
即
AC=DF
在△ABC和△
DEF
中BC=EF(已知)
∠
EFD
=∠BCA
(已知)AC=DF(已证)
∴△ABC≌△
DEF(SAS)
分析:据已知条件首先证得AC=DF,再根据已知∠EFD=∠BCA,BC=EF,根据SAS即可判定△ABC≌△DEF.
解答:解:∵AF=DC(已知),
∴AF+FC=DC+CF.
即AC=DF.
在△ABC和△DEF中
BC=EF(已知),
∠EFD=∠BCA(已知),
AC=DF(已证),
∴△ABC≌△DEF(SAS).
∴AF+FC=DC+CF.
即AC=DF.
在△ABC和△DEF中
BC=EF(已知),
∠EFD=∠BCA(已知),
AC=DF(已证),
∴△ABC≌△DEF(SAS).
点评:本题主要考查三角形全等的判定,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
相关题目
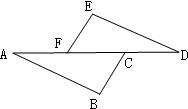
 20、如图,已知∠EFD=∠BCA,BC=EF,AF=DC.线段AB和线段DE平行吗?请说明理由.
20、如图,已知∠EFD=∠BCA,BC=EF,AF=DC.线段AB和线段DE平行吗?请说明理由.


