题目内容
22、如图,已知∠EFD=∠BCA,BC=EF,AF=DC.则AB=DE.请说明理由.(填空)
解:∵AF=DC(已知)
∴AF+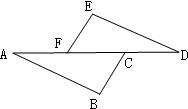
即
在△ABC和△D E F中
BC=EF(已知)
∠
∴△ABC≌△
∴AB=DE(
解:∵AF=DC(已知)
∴AF+
FC
=DC+CF

即
AC=FD
在△ABC和△D E F中
BC=EF(已知)
∠
EFD
=∠BCA
(已知
)AC=FD
∴△ABC≌△
△DEF
(SAS
)∴AB=DE(
全等三角形对应边相等
)分析:先根据等式的性质得,AC=FD,再根据SAS证明△ABC≌△DEF,利用全等三角形对应边相等得AB=DE.
解答:解:∵AF=DC(已知)
∴AF+FC=DC+CF
即AC=FD
在△ABC和△D E F中BC=EF(已知)∠EFD=∠BCA(已知) AC=FD
∴△ABC≌△△DEF( SAS)
∴AB=DE(全等三角形对应边相等)
∴AF+FC=DC+CF
即AC=FD
在△ABC和△D E F中BC=EF(已知)∠EFD=∠BCA(已知) AC=FD
∴△ABC≌△△DEF( SAS)
∴AB=DE(全等三角形对应边相等)
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
 20、如图,已知∠EFD=∠BCA,BC=EF,AF=DC.则AB=DE.请说明理由.(填空)
20、如图,已知∠EFD=∠BCA,BC=EF,AF=DC.则AB=DE.请说明理由.(填空) 20、如图,已知∠EFD=∠BCA,BC=EF,AF=DC.线段AB和线段DE平行吗?请说明理由.
20、如图,已知∠EFD=∠BCA,BC=EF,AF=DC.线段AB和线段DE平行吗?请说明理由.


