题目内容
如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.(1)请完成如下操作:
①以点O为原点、网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD.
(2)请在(1)的基础上,完成下列填空:
①写出点的坐标:C______、D______;
②⊙D的半径=______

【答案】分析:(1)根据点的坐标的表示,C的坐标即可得到,首先作出弦AB与BC的中垂线,中垂线的交点就是D,即可确定点D的坐标;
(2)①根据(1)中的平面直角坐标系直接填空;
②在直角△AOD中,利用勾股定理即可求解;
(3)连接AC、OC.过C作CH⊥AO于点H,过点A作AM⊥CO于点M.利用三角形AOC的面积等积转换求得AM的长度,然后在
Rt△AMC中利用正弦函数的定义求得∠ACO的正弦值.
解答: 解:(1)直角坐标系、点D的在该坐标系中的位置如图所示:
解:(1)直角坐标系、点D的在该坐标系中的位置如图所示:
(2)解:①根据图示知,C(6,2),D(2,0),
故答案为:(6,2),(2,0);
②解:在直角△AOD中,根据勾股定理知⊙D的半径AD= =
= =2
=2 ,
,
故答案为:2 ;
;
(3)解:连接AC、OC.过C作CH⊥AO于点H,过点A作AM⊥CO于点M.
则 OA•CH=
OA•CH= OC•AM,即
OC•AM,即 ×4×6=
×4×6= ×2
×2 •AM,
•AM,
解得,AM= ;
;
在Rt△AMC中,sin∠ACO= =
= =
= .
.
点评:本题考查了圆的综合题.涉及的知识有:坐标与图形性质,垂径定理,勾股定理,利用了数形结合的思想,根据题意画出相应的图形是解本题的关键.
(2)①根据(1)中的平面直角坐标系直接填空;
②在直角△AOD中,利用勾股定理即可求解;
(3)连接AC、OC.过C作CH⊥AO于点H,过点A作AM⊥CO于点M.利用三角形AOC的面积等积转换求得AM的长度,然后在
Rt△AMC中利用正弦函数的定义求得∠ACO的正弦值.
解答:
 解:(1)直角坐标系、点D的在该坐标系中的位置如图所示:
解:(1)直角坐标系、点D的在该坐标系中的位置如图所示:(2)解:①根据图示知,C(6,2),D(2,0),
故答案为:(6,2),(2,0);
②解:在直角△AOD中,根据勾股定理知⊙D的半径AD=
 =
= =2
=2 ,
,故答案为:2
 ;
;(3)解:连接AC、OC.过C作CH⊥AO于点H,过点A作AM⊥CO于点M.
则
 OA•CH=
OA•CH= OC•AM,即
OC•AM,即 ×4×6=
×4×6= ×2
×2 •AM,
•AM,解得,AM=
 ;
;在Rt△AMC中,sin∠ACO=
 =
= =
= .
.点评:本题考查了圆的综合题.涉及的知识有:坐标与图形性质,垂径定理,勾股定理,利用了数形结合的思想,根据题意画出相应的图形是解本题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
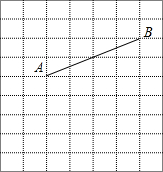 如图,在单位长度为1的正方形网格中,把线段AB绕点A顺时针旋转90°得到线段AB′.
如图,在单位长度为1的正方形网格中,把线段AB绕点A顺时针旋转90°得到线段AB′.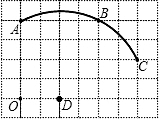 如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.以点O为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系,该圆弧所在圆的圆心为点D.
如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.以点O为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系,该圆弧所在圆的圆心为点D.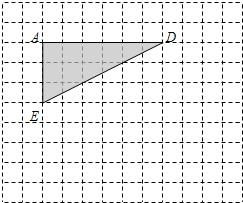 如图,在单位长度为1的正方形网格中有一个△DAE(∠DAE=90°).
如图,在单位长度为1的正方形网格中有一个△DAE(∠DAE=90°). 作图、证明与计算
作图、证明与计算 (2012•杨浦区二模)如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
(2012•杨浦区二模)如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.