题目内容
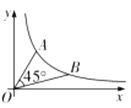
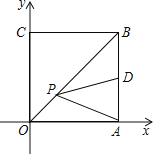
【题目】如图①，已知点
为正方形
的对角线的交点，点
是对角线
上的一个动点（点不与
重合），分别过点向直线
作垂线，垂足分别为点
，连接
和
.
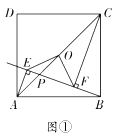
（1）求证：
；
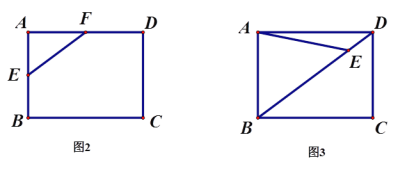
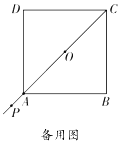
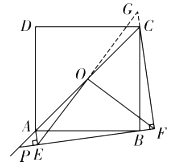
（2）如图②，延长正方形对角线
，当点运动到的延长线上时，通过证明判断（1）中的结论是否仍然成立；
（3）若点在射线
上运动，
，求线段的长.
【答案】（1）见解析；（2）
仍然成立；证明见解析；（3）OE的长为
或
.
【解析】
（1）延长EO交CF于点G，易证
和
，所以
，
即点O为EG的中点，再根据直角三角形斜边上的中线等于斜边的一半即可解答；
（2），仍然成立，延长EO和FC，相交于点G，方法同（1）即可证明；
（3）要分类讨论，①当点P在线段OA上时，易得
，所以
，在
中， 
，所以
；当点P在线段OA的延长线上时，方法同①即可解答.
（1）证明：如图，延长EO交CF于点G，
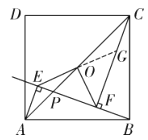
∵点O为正方形ABCD的对角线的交点，
，
，
，
，
在
和△
中，
，
，
，
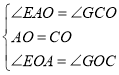即点O为EG的中点，
在中，
是斜边EG上的中线，
，
；
（2），仍然成立，
证明：如图，延长EO和FC，相交于点G，
∴点O为正方形ABCD的对角线的交点，
，
，
，
在和中，，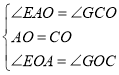
，
，
即点O为EG的中点，
在
中，
是斜边EG上的中线，
，
仍然成立；
（3）解：①当点P在线段OA上时，如图
，
.
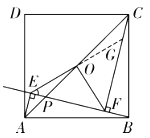
易得，
.
在中，
，
；
②当点P在线段OA的延长线上时，如图.
，.
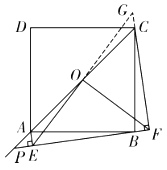
同理可得
.
在中，，
，
.
综上可知，OE的长为或.
练习册系列答案
名校课堂系列答案
相关题目
