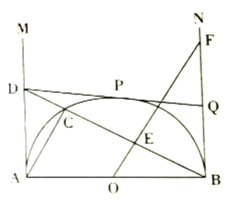
题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以每秒
上一动点,以每秒![]() 个单位长度的速度从
个单位长度的速度从![]() 出发向
出发向![]() 运动,以
运动,以![]() ,
,![]() 为边作矩形
为边作矩形![]() ,直线
,直线![]() 与直
与直![]() 、
、![]() 的交点分别为
的交点分别为![]() ,
,![]() .设点
.设点![]() 运动的时间为
运动的时间为![]() .
.

(1)![]() ______(用含
______(用含![]() 的代数式表示).
的代数式表示).
(2)当四边形![]() 是正方形时,求
是正方形时,求![]() 的长.
的长.
(3)当![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)分点D在线段BC上和在线段BC的延长线上两种情形解答即可;
(2)先有正方形的性质得到AE=![]() ,
, ![]() ,
,![]() ;说明
;说明![]() ,再根据相似三角形的性质和勾股定理求得DG、BG、EG、AG的长,然后再说明
,再根据相似三角形的性质和勾股定理求得DG、BG、EG、AG的长,然后再说明![]() ,最后利用相似三角形的性质列式计算即可;
,最后利用相似三角形的性质列式计算即可;
(3)分GF=DG和DG=DF两种情形分别构建方程求解即可.
解:(1)由题意:当0≤1≤3时,BD=CB-CD=6-2t;
当1>3时,BD=2t-6
∴BD=![]()
故答案为![]() ;
;
(2)如图,点在线段BC的延长
∵四边形![]() 是正方形时,
是正方形时,
∴AE=![]() ,
, ![]()
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
∴EG=DE+DG=8+![]() =
=![]()
∵在Rt△AEG中,EG=![]() ,AE=8
,AE=8
![]() ,
,
∵![]()
∴![]() ,
,
∴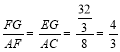
∴![]() ;
;

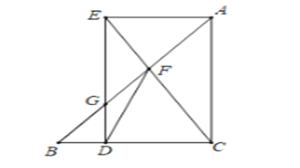
(3)在![]() 中,
中,![]() ,如图:当点
,如图:当点![]() 在线段
在线段![]() 上时,此时只有
上时,此时只有![]() ,
,
![]() ,
,
![]() ,设
,设![]() ,则
,则![]() ,
,![]()
![]() ,则
,则![]()
![]()
![]()
![]()
![]()
![]() .
.
![]() 或
或![]() (舍去),
(舍去),
![]() ,
,
![]() ,
,
![]() ;
;
如图:当点![]() 在线段
在线段![]() 的延长线上时,此时只有
的延长线上时,此时只有![]() ,作
,作![]() 于
于![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
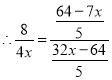 ,
,
![]() (负数舍去),
(负数舍去),
![]() ,
,
![]() ,
,
综上,当![]() 为等腰三角形时,
为等腰三角形时,![]() 为
为![]() 或
或![]() .
.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案【题目】钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答年新型冠状病毒防治全国统一考试全国卷试卷满分![]() 分,社区管理员随机从有
分,社区管理员随机从有![]() 人的某小区抽取
人的某小区抽取![]() 名人员的答卷成绩,根据他们的成绩数据绘制了如下的表格和统计图:
名人员的答卷成绩,根据他们的成绩数据绘制了如下的表格和统计图:
等级 | 成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
| |
根据上面提供的信息,回答下列问题: .
(1)统计表中的![]() ,
,![]() ,
,![]() ;
;
(2)请补全条形统计图;
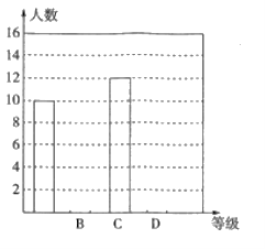
(3)根据抽样调查结果,请估计该小区答题成绩为“![]() 级”的有多少人?
级”的有多少人?
【题目】时代中学从学生兴趣出发,实施体育活动课走班制.为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1200名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 |
| 15 | 33 |
|
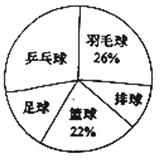
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,![]() ________,
________,![]() ________;
________;
(3)试估计上述1200名学生中最喜欢乒乓球运动的人数.