题目内容
 如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B.
如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B.(1)抛物线的对称轴为
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时,设△PBQ的面积为S,求S与t之间的函数关系式(要求写出t的取值范围)
②当S取得最大值时,点P的坐标是
考点:二次函数综合题
专题:
分析:(1)由矩形的性质可以得出AB、BC的值就由得出A、B的坐标,根据抛物线的对称性及可以对称轴;
(2)①根据三角形的面积公式就可以直接表示出S与t之间的函数关系式;
②将①的解析式化为顶点式,就可以求出S的最大值时t的值,从而可以求出结论.
(2)①根据三角形的面积公式就可以直接表示出S与t之间的函数关系式;
②将①的解析式化为顶点式,就可以求出S的最大值时t的值,从而可以求出结论.
解答:解:(1)∵四边形OABC是矩形,
∴OA=BC,OC=AB.
∴OA=12cm,OC=6cm,
∴BC=12cm,AB=6cm,
∴B(6,-12),A(0,-12),
∴对称轴x=3.
(2)①由题意,得
AP=t,BQ=2t,
∴BP=6-t.
∵S△BPQ=
,
∴S=
=-t2+6t(0<t<6);
②∵S=-t2+6t,
∴S=-(t-3)2+9,
∴a=-1<0,
∴t=3时,S最大=9,
∴AP=3,BQ=6,
∴CQ=6,
∴P(3,-12),Q(6,-6).
故答案为:x=3,(6,-12);(3,-12),(6,-6).
∴OA=BC,OC=AB.

∴OA=12cm,OC=6cm,
∴BC=12cm,AB=6cm,
∴B(6,-12),A(0,-12),
∴对称轴x=3.
(2)①由题意,得
AP=t,BQ=2t,
∴BP=6-t.
∵S△BPQ=
| BP•BQ |
| 2 |
∴S=
| 2t(6-t) |
| 2 |
②∵S=-t2+6t,
∴S=-(t-3)2+9,
∴a=-1<0,
∴t=3时,S最大=9,
∴AP=3,BQ=6,
∴CQ=6,
∴P(3,-12),Q(6,-6).
故答案为:x=3,(6,-12);(3,-12),(6,-6).
点评:本题考查了矩形的性质的运用,抛物线的图象性质的运用,三角形的面积公式的运用,二次函数的顶点式的运用,解答本题时灵活运用二次函数的图象及解析式的性质是关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
下列说法错误的是( )
| A、无理数与有理数的和是无理数 |
| B、无理数与有理数的积是无理数 |
| C、无理数的相反数是无理数 |
| D、无理数的绝对值是无理数 |
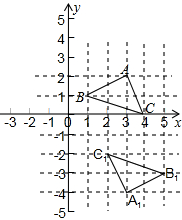 如图,在平面直角坐标系中,若△BAC与△A1B1C1关于点E成中心对称,则对称中心点E的坐标是( )
如图,在平面直角坐标系中,若△BAC与△A1B1C1关于点E成中心对称,则对称中心点E的坐标是( )| A、(2,-1) |
| B、(3,-1) |
| C、(4,-1) |
| D、(3,-2) |
在-3,0,-
,3四个数中,最小的数是( )
| 3 |
| A、3 | ||
| B、0 | ||
C、-
| ||
| D、-3 |
 如图,已知二次函数y=ax2+bx+c的图象经过点A(3,0),B(2,-3),C(0,-3).
如图,已知二次函数y=ax2+bx+c的图象经过点A(3,0),B(2,-3),C(0,-3). 如图,在等腰Rt△ABC中,且∠C=90°,CD=2,BD=3,D、E分别是BC、AC边上的点,将DE绕D点顺时针旋转90°,E点刚好落在AB边上的F点处,则CE=
如图,在等腰Rt△ABC中,且∠C=90°,CD=2,BD=3,D、E分别是BC、AC边上的点,将DE绕D点顺时针旋转90°,E点刚好落在AB边上的F点处,则CE=