题目内容
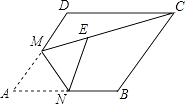
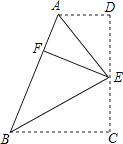
【题目】如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为 . 
【答案】![]() 或
或 ![]()
![]()
【解析】解:如图 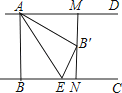 ,
,
由翻折的性质,得
AB=AB′,BE=B′E.
①当MB′=2,B′N=1时,设EN=x,得
B′E= ![]() .
.
△B′EN∽△AB′M,![]() ,即
,即 ![]() =
= ![]() ,x2=
,x2= ![]() ,BE=B′E=
,BE=B′E= ![]() =
= ![]() .
.
②当MB′=1,B′N=2时,设EN=x,得
B′E= ![]() ,
,
△B′EN∽△AB′M,![]() ,即
,即 ![]() =
= ![]() ,解得x2=
,解得x2= ![]() ,BE=B′E=
,BE=B′E= ![]() =
= ![]() ,
,
故答案为: ![]() 或
或 ![]() .
.
根据勾股定理,可得EB′,根据相似三角形的性质,可得EN的长,根据勾股定理,可得答案.本题考查了翻折的性质,利用翻折的性质得出AB=AB′,BE=B′E是解题关键,又利用了相似三角形的性质,要分类讨论,以防遗漏.

练习册系列答案
相关题目