题目内容
18. 如图,两个正方形的面积分别为64和49,则AC等于( )
如图,两个正方形的面积分别为64和49,则AC等于( )| A. | 15 | B. | 17 | C. | 23 | D. | 113 |
分析 根据正方形的性质求出AB、BD、DC的长,再根据勾股定理求出AC的长即可.
解答  解:∵两个正方形的面积分别是64和49,
解:∵两个正方形的面积分别是64和49,
∴AB=BD=8,DC=7,
根据勾股定理得:AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=17.
故选B.
点评 本题考查了勾股定理,求出AB、BC的长并熟悉勾股定理是解题的关键.

练习册系列答案
相关题目
13.一元二次方程:x2-9=0的解是( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 9 |
7.把$\sqrt{18}$化成最简二次根式,结果为( )
| A. | $2\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | $3\sqrt{6}$ | D. | $9\sqrt{2}$ |
 已知:如图AB⊥BD,CD⊥BD,AB=DC,求证:AD∥BC.
已知:如图AB⊥BD,CD⊥BD,AB=DC,求证:AD∥BC.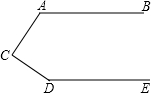 如图,AB∥DE,∠A=120°,∠C=80°,则∠D的度数为160°.
如图,AB∥DE,∠A=120°,∠C=80°,则∠D的度数为160°.