题目内容
若两个实数a,b,使得,a2+b与a+b2都是有理数,称数对(a,b)是和谐的.①试找出一对无理数,使得(a,b)是和谐的;
②证明:若(a,b)是和谐的,且a+b是不等于1的有理数,则a,b都是有理数;
③证明:若(a,b)是和谐的,且
| a | b |
分析:①假设a=
+
,b=
-
,再求出a2+b与a+b2的值,在进行判断即可;
②根据题意可知t=(a2+b)-(a+b2)=(a-b)(a+b-1)是有理数,a+b=s是有理数,进而可用s表示出a,根据a是有理数即可判断出b也是有理数;
③由于a、b的值不能确定,故可分a+b2=0和a+b2≠0两种情况进行判断.
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
②根据题意可知t=(a2+b)-(a+b2)=(a-b)(a+b-1)是有理数,a+b=s是有理数,进而可用s表示出a,根据a是有理数即可判断出b也是有理数;
③由于a、b的值不能确定,故可分a+b2=0和a+b2≠0两种情况进行判断.
解答:解:①假设a=
+
,b=
-
,则a2+b=(
+
)2+
-
=
是有理数,
a+b2=
+
+(
-
)2=
是有理数,
故(a,b)=(
+
,
-
)是和谐的;
②由已知t=(a2+b)-(a+b2)=(a-b)(a+b-1)是有理数,a+b=s是有理数,
因此a-b=
,解得a=
(s+
)是有理数,
当然b=s-a也是有理数;
③若a+b2=0,则b=-
是有理数,因此a=(a+b2)-b2也是有理数.
若a+b2≠0,由已知x=
=
是有理数,y=
也是有理数,
因此
=
,故b=
是有理数,
因此a=(a+b2)-b2也是有理数.
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 11 |
| 4 |
a+b2=
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 11 |
| 4 |
故(a,b)=(
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
②由已知t=(a2+b)-(a+b2)=(a-b)(a+b-1)是有理数,a+b=s是有理数,
因此a-b=
| t |
| a+b-1 |
| 1 |
| 2 |
| t |
| s-1 |
当然b=s-a也是有理数;
③若a+b2=0,则b=-
| a |
| b |
若a+b2≠0,由已知x=
| a2+b |
| a+b2 |
(
| ||||
|
| a |
| b |
因此
| 1 |
| b |
| y2-x |
| xy-1 |
| xy-1 |
| y2-x |
因此a=(a+b2)-b2也是有理数.
点评:本题考查的是无理数及有理数的概念及运算,熟知无理数及有理数的概念是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
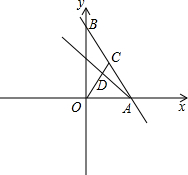 在平面直角坐标系中,点A、B分别在x轴、y 轴上,线段OA、OB的长(OA<OB)是关于x的方程x2-(2m+6)x+2m2=0的两个实数根,C是线段AB的中点,OC=3
在平面直角坐标系中,点A、B分别在x轴、y 轴上,线段OA、OB的长(OA<OB)是关于x的方程x2-(2m+6)x+2m2=0的两个实数根,C是线段AB的中点,OC=3