Question

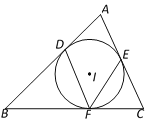
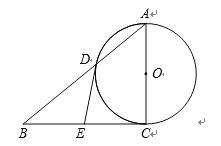
【题目】如图，⊙O是△ABC的外接圆，AB是⊙O的直径，D是的中点，AD交BC于点E，若CE＝，BE＝，以下结论中：①sin∠ABC＝；②AD＝，③S⊙O＝π；④OE∥BD．其中正确的共有（　　）个．

A.1B.2C.3D.4

Answer 1

【答案】D

【解析】

①根据已知得BC=CE+BE=2，连接OD，根据垂径定理得：OD⊥BC，CF=BF=，则EF=﹣＝，证明△ACE≌△DFE，设OF=x，则AC=2x，OD=3x，根据三角函数定义可得结论；

②根据勾股定理可得：AC=1，计算AE的长，可得AD的长；

③由②知：AB2=（3AC）2=9，根据圆的面积公式计算即可；

④根据△ACE≌△DFE，可得AE=ED，利用三角形中位线定理可得结论．

①∵CE＝，BE＝，

∴BC＝CE+BE＝2，

连接OD，交BC于点F，

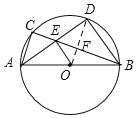
∵D是的中点，

∴OD⊥BC，CF＝BF＝，

∴EF＝﹣＝，

∵AB是⊙O的直径，

∴∠ACB＝90°，

在△ACE和△DFE中，

∵，

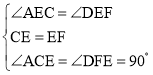∴△ACE≌△DFE（ASA），

∴AC＝DF

∵OF是△ABC的中位线，

∴AC＝DF＝2OF，

设OF＝x，则AC＝DF＝2x，OD＝3x，

∴AB＝6x，

Rt△ACB中，sin∠ABC＝＝＝；

故①正确；

②Rt△ACB中，AC2+BC2＝AB2，

（2x）2+（2）2＝（6x）2，

x＝，

∴AC＝2x＝1，

由勾股定理得：AE＝＝＝，

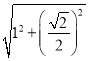∴AD＝2AE＝；

故②正确；

③由②知：AB2＝（3AC）2＝9，

∴S⊙O＝π＝＝，

故③正确；

④∵△ACE≌△DFE，

∴AE＝ED，

∵AO＝OB，

∴OE∥BD，

故④正确；

本题正确的结论有：①②③④，4个

故选：D．