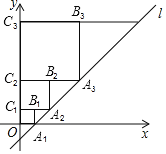
ЬтФПФкШн
ЁОЬтФПЁПЖЈвхЃКдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() ЃЈ
ЃЈ![]() ЃЉгыжБЯп
ЃЉгыжБЯп![]() НЛгкЕу
НЛгкЕу![]() ЁЂ
ЁЂ![]() ЃЈЕу
ЃЈЕу![]() дкЕу
дкЕу![]() гвБпЃЉЃЌНЋХзЮяЯп
гвБпЃЉЃЌНЋХзЮяЯп![]() бижБЯп
бижБЯп![]() ЗелЃЌЗелЧАКѓСНХзЮяЯпЕФЖЅЕуЗжБ№ЮЊЕу
ЗелЃЌЗелЧАКѓСНХзЮяЯпЕФЖЅЕуЗжБ№ЮЊЕу![]() ЁЂ
ЁЂ![]() ЃЌЮвУЧНЋСНХзЮяЯпжЎМфаЮГЩЕФЗтБеЭМаЮГЦЮЊОЊЯВЯпЃЌЫФБпаЮ
ЃЌЮвУЧНЋСНХзЮяЯпжЎМфаЮГЩЕФЗтБеЭМаЮГЦЮЊОЊЯВЯпЃЌЫФБпаЮ![]() ГЦЮЊОЊЯВЫФБпаЮЃЌЖдНЧЯп
ГЦЮЊОЊЯВЫФБпаЮЃЌЖдНЧЯп![]() гы
гы![]() жЎБШГЦЮЊОЊЯВЖШЃЈDegree of surpriseЃЉЃЌМЧзї
жЎБШГЦЮЊОЊЯВЖШЃЈDegree of surpriseЃЉЃЌМЧзї![]() .
.
ЃЈ1ЃЉШчЭМЃЈ1ЃЉХзЮяЯп![]() бижБЯп
бижБЯп![]() ЗелКѓЕУЕНОЊЯВЯп.дђЕу
ЗелКѓЕУЕНОЊЯВЯп.дђЕу![]() зјБъ ЃЌЕу
зјБъ ЃЌЕу![]() зјБъ ЃЌОЊЯВЫФБпаЮ
зјБъ ЃЌОЊЯВЫФБпаЮ![]() ЪєгкЫљбЇЙ§ЕФФФжжЬиЪтЦНааЫФБпаЮЃП ЃЌ
ЪєгкЫљбЇЙ§ЕФФФжжЬиЪтЦНааЫФБпаЮЃП ЃЌ![]() ЮЊ .
ЮЊ .
ЃЈ2ЃЉШчЙћХзЮяЯп![]() ЃЈ
ЃЈ![]() ЃЉбижБЯп
ЃЉбижБЯп![]() ЗелКѓЫљЕУОЊЯВЯпЕФОЊЯВЖШЮЊ1ЃЌЧѓ
ЗелКѓЫљЕУОЊЯВЯпЕФОЊЯВЖШЮЊ1ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ЃЈ3ЃЉШчЙћХзЮяЯп![]() бижБЯп
бижБЯп![]() ЗелКѓЫљЕУЕФОЊЯВЯпдк
ЗелКѓЫљЕУЕФОЊЯВЯпдк![]() ЪБЃЌЦфзюИпЕуЕФзнзјБъЮЊ16ЃЌЧѓ
ЪБЃЌЦфзюИпЕуЕФзнзјБъЮЊ16ЃЌЧѓ![]() ЕФжЕВЂжБНгаДГіОЊЯВЖШ
ЕФжЕВЂжБНгаДГіОЊЯВЖШ![]() .
.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛ
ЃЛ![]() ЃЛСтаЮЃЛ2ЃЛЃЈ2ЃЉ
ЃЛСтаЮЃЛ2ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЌ
ЃЌ![]() Лђ
Лђ![]() ЃЌ
ЃЌ![]() .
.
ЁОНтЮіЁП
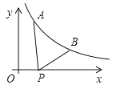
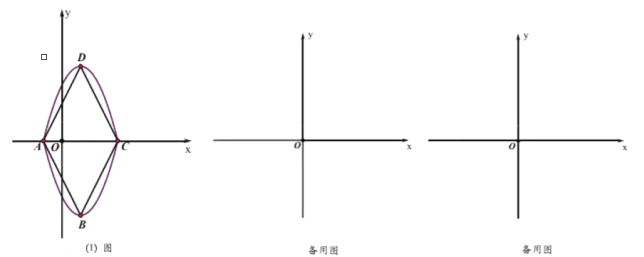
ЃЈ1ЃЉЕБy=0ЪБПЩЧѓГіЕуAзјБъЮЊ![]() ЃЌBзјБъЮЊ
ЃЌBзјБъЮЊ![]() ЃЌAB=4ЃЌИљОнЫФБпаЮЫФБпЯрЕШПЩжЊИУЫФБпаЮЮЊСтаЮЃЌгЩ
ЃЌAB=4ЃЌИљОнЫФБпаЮЫФБпЯрЕШПЩжЊИУЫФБпаЮЮЊСтаЮЃЌгЩ![]() ПЩжЊХзЮяЯпЖЅЕузјБъЮЊЃЈ1ЃЌ-4ЃЉЃЌЫљвдB
ПЩжЊХзЮяЯпЖЅЕузјБъЮЊЃЈ1ЃЌ-4ЃЉЃЌЫљвдB![]() ЃЌAB=8ЃЌМДПЩЕУЕН
ЃЌAB=8ЃЌМДПЩЕУЕН![]() ЮЊ2ЃЛ
ЮЊ2ЃЛ
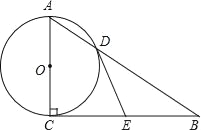
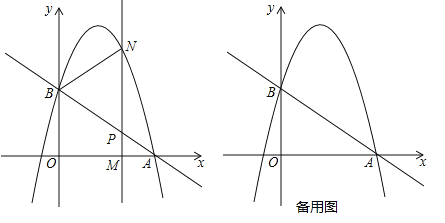
ЃЈ2ЃЉОЊЯВЖШЮЊ1МД![]() ЃЌРћгУХзЮяЯпНтЮіЪНЗжБ№ЧѓГіИїЕузјБъЃЌДгЖјЕУЕНACКЭBDЕФГЄЃЌМЦЫуМДПЩЧѓГіmЃЛ
ЃЌРћгУХзЮяЯпНтЮіЪНЗжБ№ЧѓГіИїЕузјБъЃЌДгЖјЕУЕНACКЭBDЕФГЄЃЌМЦЫуМДПЩЧѓГіmЃЛ
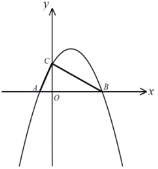
ЃЈ3ЃЉЯШЧѓГіЖЅЕузјБъ![]() ЃЌЖдГЦжсЮЊжБЯп
ЃЌЖдГЦжсЮЊжБЯп![]() ЃЌЬжТлЖдГЦжсжБЯп
ЃЌЬжТлЖдГЦжсжБЯп![]() ЪЧЗёдк
ЪЧЗёдк![]() етИіЗЖЮЇФкЃЌЗж3жаЧщПіЗжБ№ЧѓГізюДѓжЕЮЊ16ЪЧmЕФжЕ.
етИіЗЖЮЇФкЃЌЗж3жаЧщПіЗжБ№ЧѓГізюДѓжЕЮЊ16ЪЧmЕФжЕ.
НтЃКЃЈ1ЃЉдкХзЮяЯп![]() ЩЯЃЌ
ЩЯЃЌ
ЕБy=0ЪБЃЌ![]() ЃЌ
ЃЌ
НтЕУЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁпЕу![]() дкЕу
дкЕу![]() гвБпЃЌ
гвБпЃЌ
ЁрAЕуЕФзјБъЮЊ![]() ЃЌBЕуЕФзјБъЮЊ
ЃЌBЕуЕФзјБъЮЊ![]() ЃЛ
ЃЛ
ЁрAB=4ЃЌ
Ёп![]()
ЁрЖЅЕуBЕФзјБъЮЊ![]() ЃЌ
ЃЌ
гЩгкBDЙигкxжсЖдГЦЃЌ
ЁрDЕФзјБъЮЊ![]() ЃЌ
ЃЌ
ЁрBD=8ЃЌ
ЭЈЙ§ХзЮяЯпЕФЖдГЦадЕУЕНAB=BCЃЌ
гжгЩгкЗелЃЌЕУЕНAB=BC=AD=CDЃЌ
ЁрОЊЯВЫФБпаЮ![]() ЮЊСтаЮЃЛ
ЮЊСтаЮЃЛ
![]() ЃЛ
ЃЛ
ЃЈ2ЃЉгЩЬтвтЕУЃК![]()
![]() ЕФЖЅЕузјБъ
ЕФЖЅЕузјБъ![]() ЃЌ
ЃЌ![]()
НтЕУЃК![]() ЃЌЁр
ЃЌЁр![]()
![]()
Ёр![]() ЃЌ
ЃЌ![]()
ЃЈ3ЃЉХзЮяЯпЕФЖЅЕуЮЊ![]() ЃЌЖдГЦжсЮЊжБЯпЃК
ЃЌЖдГЦжсЮЊжБЯпЃК![]()
Ђй![]() МД
МД![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЕУ
ЃЌЕУ![]()
Ёр![]()
Ђк![]() МД
МД![]() ЪБЃЌ
ЪБЃЌ![]() ЪБЃЌЖдгІОЊЯВЯпЩЯзюИпЕуЕФКЏЪ§жЕ
ЪБЃЌЖдгІОЊЯВЯпЩЯзюИпЕуЕФКЏЪ§жЕ![]()
![]() ЃЌЁр
ЃЌЁр![]() ЃЈЩсШЅЃЉЃЛ
ЃЈЩсШЅЃЉЃЛ![]()
Ёр![]()
Ђл![]() МД
МД![]() ЪБаЮГЩВЛСЫОЊЯВЯпЃЌЙЪВЛДцдк
ЪБаЮГЩВЛСЫОЊЯВЯпЃЌЙЪВЛДцдк![]()
злЩЯЫљЪіЃЌ![]() ЃЌ
ЃЌ![]() Лђ
Лђ![]() ЃЌ
ЃЌ![]()