Question

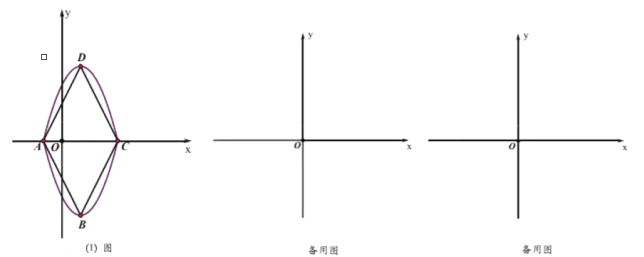
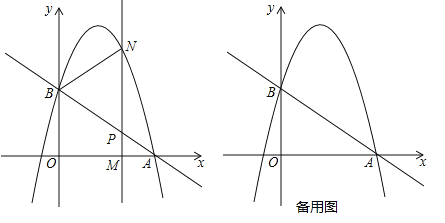
【题目】如图，抛物线过点和，点为线段上一个动点(点与点不重合)，过点作垂直于轴的直线与直线和抛物线分别交于点．

（1）求此抛物线的解析式；

（2）若点是的中点，则求点的坐标；

（3）若以点为顶点的三角形与相似，请直接写出点的坐标．

Answer 1

【答案】（1）；（2）；（3）P(,)或P(,)

【解析】

(1)把A点坐标和B点坐标代入，解方程组即可；

(2)用m可表示出P、N的坐标，由题意可知有P为线段MN的中点，可得到关于m的方程，可求得m的值，即可求得点的坐标；

(3) 用m可表示出NP,PM,AM,分当∠BNP=90°时和当∠NBP=90°时两种情况讨论即可.

解： (1) 抛物线经过点

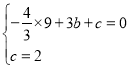解得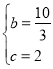

∴

(2)由题意易得，直线的解析式为

由，设，

则，

点是的中点，即

∴，解得 (舍)

∴

(3) ．

由，设，

∴，，AM=3m，
∵△BPN和△APM相似，且∠BPN=∠APM，
∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°，
当∠BNP=90°时，则有BN⊥MN，
∴N点的纵坐标为2，
∴=2，
解得m=0(舍去)或m=，
∴P(,)；
当∠NBP=90°时，过点N作NC⊥y轴于点C，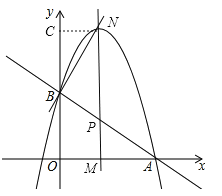

则∠NBC+∠BNC=90°，NC=m，BC=2=，
∵∠NBP=90°，
∴∠NBC+∠ABO=90°，
∴∠ABO=∠BNC，
∴Rt△NCB∽Rt△BOA，
∴，
∴m2=，
解得m=0(舍去)或m=，
∴P(,),
综上可知，当以B，P，N为顶点的三角形与△APM相似时，点P的坐标为P(,)或P(,)．